题目内容
【题目】在棱长为![]() 的透明密闭的正方形容器
的透明密闭的正方形容器![]() 中,装有容器总体积一半的水(不计容器壁的厚度),将该正方体容器绕
中,装有容器总体积一半的水(不计容器壁的厚度),将该正方体容器绕![]() 旋转,并始终保持
旋转,并始终保持![]() 所在直线与水平平面平行,则在旋转过程中容器中水的水面面积的最大值为__________.
所在直线与水平平面平行,则在旋转过程中容器中水的水面面积的最大值为__________.
【答案】![]()
【解析】
设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,满足
上,满足![]() ,则原问题等价于求解四边形
,则原问题等价于求解四边形![]() 的最大值.建立空间直角坐标系,结合二次函数的性质可得旋转过程中容器中水的水面面积的最大值.
的最大值.建立空间直角坐标系,结合二次函数的性质可得旋转过程中容器中水的水面面积的最大值.
如图所示,在棱长为![]() 的正方体
的正方体![]() 中,
中,
点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,满足
上,满足![]() ,
,
则原问题等价于求解四边形![]() 的最大值.
的最大值.
作![]() 于点
于点![]() ,当
,当![]() 最大时,四边形
最大时,四边形![]() 有最大值.
有最大值.
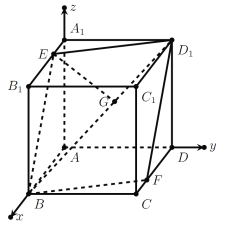
建立如图所示的空间直角坐标系,
设![]() ,设
,设![]() ,
,
由于![]() ,由
,由![]() 可得:
可得:
![]() ,则:
,则: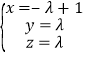 ,故
,故![]() ,
,
故:![]() ,
,
由![]() 可得:
可得:![]() .
.
故:![]()
![]() ,
,
结合二次函数的性质可知:当![]() 或
或![]() 时,
时,![]() 取得最大值,此时
取得最大值,此时![]() 取得最大值,最大值为:
取得最大值,最大值为:![]() .
.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目