题目内容
设函数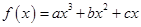 在区间
在区间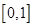 上是增函数,在区间
上是增函数,在区间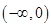 ,
,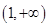 上是减函数,又
上是减函数,又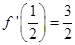
(1)求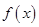 的解析式;
的解析式;
(2)若在区间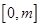
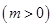 上恒有
上恒有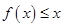 成立,求
成立,求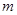 的取值范围
的取值范围
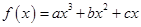 在区间
在区间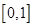 上是增函数,在区间
上是增函数,在区间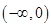 ,
,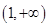 上是减函数,又
上是减函数,又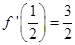
(1)求
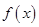 的解析式;
的解析式;(2)若在区间
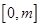
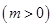 上恒有
上恒有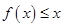 成立,求
成立,求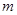 的取值范围
的取值范围(1)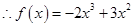 (2)
(2)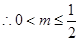
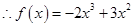 (2)
(2)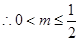
试题分析:解:(1)
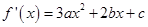 1分
1分由已知
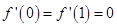 ,即
,即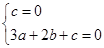 3分
3分解得
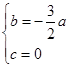 4分
4分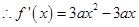
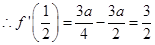
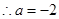
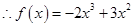 7分
7分(2)令
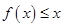 ,即
,即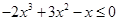
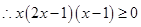
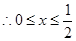 或
或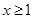
又
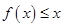 在区间
在区间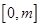 上恒成立,
上恒成立,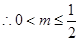 14分
14分点评:解决的关键是通过导数的值来求解解析式,以积极通过不等式的求解得到参数的范围,属于中档题。

练习册系列答案
相关题目
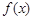 =x+ax2+blnx,曲线y=
=x+ax2+blnx,曲线y=
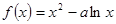 在(1,2)上是增函数,
在(1,2)上是增函数,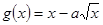 在(0,1)上是减函数。
在(0,1)上是减函数。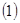 求
求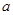 的值;
的值;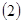 当
当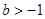 时,若
时,若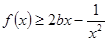 在
在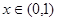 内恒成立,求实数
内恒成立,求实数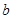 的取值范围;
的取值范围;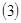 求证:方程
求证:方程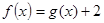 在
在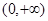 内有唯一解.
内有唯一解.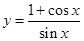 在点
在点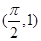 处的切线与直线
处的切线与直线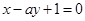 平行,则实数
平行,则实数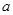 等于( )
等于( )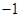
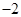
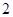
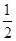
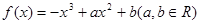
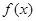 在区间(0,1)上单调递增,试求a的取值范围;
在区间(0,1)上单调递增,试求a的取值范围;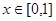 时,
时,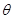 ,试求当
,试求当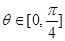 时,a的取值范围.
时,a的取值范围.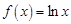 ,若存在
,若存在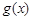 使得
使得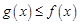 恒成立,则称
恒成立,则称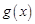 是
是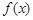 的
的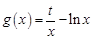 (t为实数)为
(t为实数)为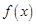 的一个“下界函数”,
的一个“下界函数”,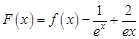 ,试问函数
,试问函数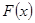 是否存在零点,若存在,求出零点个数;
是否存在零点,若存在,求出零点个数;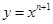 (
(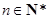 )在点(1,1)处的切线与x轴的交点的横坐标为
)在点(1,1)处的切线与x轴的交点的横坐标为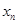 ,则
,则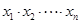 = .
= .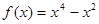 ,那么
,那么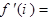 ( ) (i是虚数单位)
( ) (i是虚数单位)