题目内容
设曲线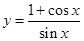 在点
在点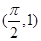 处的切线与直线
处的切线与直线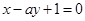 平行,则实数
平行,则实数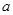 等于( )
等于( )
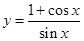 在点
在点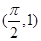 处的切线与直线
处的切线与直线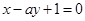 平行,则实数
平行,则实数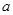 等于( )
等于( )A.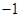 | B.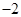 | C.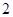 | D.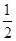 |
A
试题分析:因为,
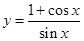 ,所以,
,所以,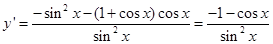 ,由曲线的切线斜率,等于在切点的导函数值。得,-1=
,由曲线的切线斜率,等于在切点的导函数值。得,-1=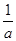 ,
,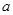 =-1,故选A。
=-1,故选A。点评:小综合题,两直线平行的必要条件是,斜率相等或斜率均不存在。曲线的切线斜率,等于在切点的导函数值。

练习册系列答案
相关题目
题目内容
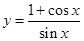 在点
在点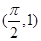 处的切线与直线
处的切线与直线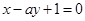 平行,则实数
平行,则实数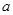 等于( )
等于( )A.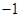 | B.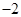 | C.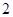 | D.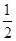 |
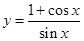 ,所以,
,所以,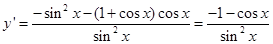 ,由曲线的切线斜率,等于在切点的导函数值。得,-1=
,由曲线的切线斜率,等于在切点的导函数值。得,-1=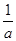 ,
,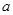 =-1,故选A。
=-1,故选A。