题目内容
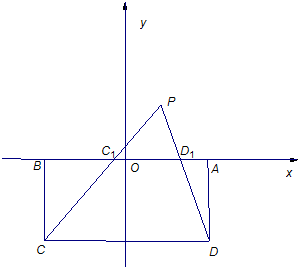 如图,矩形ABCD中,|AB|=10,|BC|=6,现以矩形ABCD的AB边为x轴,AB的中点为原点建立直角坐标系,P是x轴上方一点,使得PC、PD与线段AB分别交于点C1、D1,且|AD1|,|D1C1|,|C1B|成等比数列.
如图,矩形ABCD中,|AB|=10,|BC|=6,现以矩形ABCD的AB边为x轴,AB的中点为原点建立直角坐标系,P是x轴上方一点,使得PC、PD与线段AB分别交于点C1、D1,且|AD1|,|D1C1|,|C1B|成等比数列.(1)求动点P的轨迹方程;
(2)求动点P到直线l:x+y+6=0距离的最大值及取得最大值时点P的坐标.
分析:(1)设点P的坐标为(x,y)(y>0),用坐标分别表示出|AD1|,|D1C1|,|C1B|,利用|AD1|,|D1C1|,|C1B|成等比数列,得方程,进而化简即可得动点P的轨迹方程;
(2)由图易知当与直线l平行的直线与半椭圆相切于点P时,点P到直线l距离的最大.设与直线l:x+y+6=0平行的直线方程为x+y+k=0,代入
+
=1,化简得 34x2+50kx+25k2-225=0,利用△=0,可求k的值.从而可求点P到直线l距离的最大值及点P的坐标.
(2)由图易知当与直线l平行的直线与半椭圆相切于点P时,点P到直线l距离的最大.设与直线l:x+y+6=0平行的直线方程为x+y+k=0,代入
| x2 |
| 25 |
| y2 |
| 9 |
解答: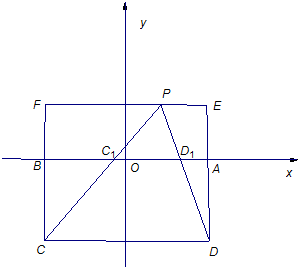 解:(1)设点P的坐标为(x,y)(y>0),过P作PE∥CD交DA的延长线于E,交CB的延长线于F.
解:(1)设点P的坐标为(x,y)(y>0),过P作PE∥CD交DA的延长线于E,交CB的延长线于F.
在△DPE中,
=
,得
=
,
得|D1A|=
.
在△PCD中,
=
=
=
,
得|C1D1|=
.
同理可得|C1B|=
.
∵|AD1|,|D1C1|,|C1B|成等比数列,
∴|D1C1|2=|AD1|•|C1B|.
∴(
)2=
•
.
化简得
+
=1(y>0).
∴动点P的轨迹方程为
+
=1(y>0).
(2)由图易知当与直线l平行的直线与半椭圆相切于点P时,点P到直线l距离的最大.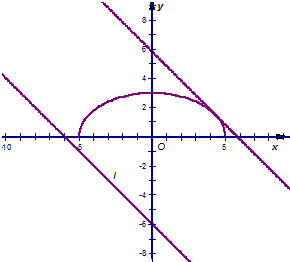
设与直线l:x+y+6=0平行的直线方程为x+y+k=0,代入
+
=1,
得 34x2+50kx+25k2-225=0,①
由△=2500k2-3400(k2-9)=0,
解得k2=34,由k<0,得k=-
.
故点P到直线l距离的最大值为
=
=3
+
.
把k=-
代入①式,可解得点P的坐标为(
,
).
 解:(1)设点P的坐标为(x,y)(y>0),过P作PE∥CD交DA的延长线于E,交CB的延长线于F.
解:(1)设点P的坐标为(x,y)(y>0),过P作PE∥CD交DA的延长线于E,交CB的延长线于F.在△DPE中,
| |D1A| |
| |PE| |
| |DA| |
| |DE| |
| |D1A| |
| 5-x |
| 6 |
| 6+y |
得|D1A|=
| 6(5-x) |
| 6+y |
在△PCD中,
| |C1D1| |
| |CD| |
| |PD1| |
| |PD| |
| |EA| |
| |ED| |
| y |
| 6+y |
得|C1D1|=
| 10y |
| 6+y |
同理可得|C1B|=
| 6(5+x) |
| 6+y |
∵|AD1|,|D1C1|,|C1B|成等比数列,
∴|D1C1|2=|AD1|•|C1B|.
∴(
| 10y |
| 6+y |
| 6(5-x) |
| 6+y |
| 6(5+x) |
| 6+y |
化简得
| x2 |
| 25 |
| y2 |
| 9 |
∴动点P的轨迹方程为
| x2 |
| 25 |
| y2 |
| 9 |
(2)由图易知当与直线l平行的直线与半椭圆相切于点P时,点P到直线l距离的最大.

设与直线l:x+y+6=0平行的直线方程为x+y+k=0,代入
| x2 |
| 25 |
| y2 |
| 9 |
得 34x2+50kx+25k2-225=0,①
由△=2500k2-3400(k2-9)=0,
解得k2=34,由k<0,得k=-
| 34 |
故点P到直线l距离的最大值为
| |k-6| | ||
|
|-
| ||
|
| 2 |
| 17 |
把k=-
| 34 |
25
| ||
| 34 |
9
| ||
| 34 |
点评:本题以等比数列为载体,考查轨迹方程的求解,考查直线与椭圆的位置关系,解题的关键是将问题转化为当与直线l平行的直线与半椭圆相切于点P时,点P到直线l距离的最大求解

练习册系列答案
相关题目
 如图,矩形ABCD中,AB=
如图,矩形ABCD中,AB=
 A 若方程ax-x-a=0有两个实数解,则a的取值范围是
A 若方程ax-x-a=0有两个实数解,则a的取值范围是 如图,矩形ABCD中,
如图,矩形ABCD中, (理)如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD
(理)如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD