题目内容
判断函数
在区间（0，+∞）上的单调性，并用单调性的定义证明结论．
【答案】分析：先在定义域上取值，再作差、变形，变形彻底后根据式子的特点，讨论判断符号、下结论．
解答：证明：设0＜x1＜x2，则有f（x1）-f（x2）=（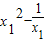
）-（
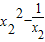）=（x1-x2）（x1+x2）-（
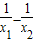）=（x1-x2）（x1+x2+
），
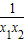∵0＜x1＜x2，
∴x1-x2＜0，x1+x2+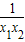
＞0，
所以f（x1）-f（x）＜0，即f（x1）＜f（x2）
所以函数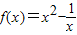
在区间（0，+∞）上是单调递增函数．
点评：本题考查了函数单调性的证明方法：定义法，关键是变形一定彻底，直到能明显的判断出符号为止．
解答：证明：设0＜x1＜x2，则有f（x1）-f（x2）=（
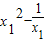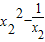）-（）=（x1-x2）（x1+x2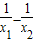）-（）=（x1-x2）（x1+x2+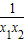），∵0＜x1＜x2，
∴x1-x2＜0，x1+x2+
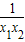＞0，所以f（x1）-f（x）＜0，即f（x1）＜f（x2）
所以函数
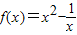在区间（0，+∞）上是单调递增函数．点评：本题考查了函数单调性的证明方法：定义法，关键是变形一定彻底，直到能明显的判断出符号为止．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
，
，
，
这几个函数值，你能发现f（x）与
有什么关系？并证明你的结论；
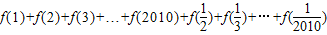的值；
在区间（0，+∞）上的单调性．
在区间（0，1）上的单调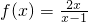性．
在区间（0，1）上的单调性.
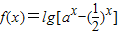，（ a＞0，a≠1，a为常数）
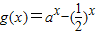在区间（0，+∞）上的单调性；
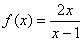在区间（0，1）上的单调性.