题目内容
已知函数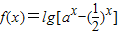 ,( a>0,a≠1,a为常数)
,( a>0,a≠1,a为常数)(1)当a=2时,求f(x)的定义域;
(2)当a>1时,判断函数
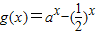 在区间(0,+∞)上的单调性;
在区间(0,+∞)上的单调性;(3)当a>1时,若f(x)在[1,+∞)上恒取正值,求a应满足的条件.
【答案】分析:(1)根据对数函数的性质可知,真数恒大于零,建立不等关系,解之即可;
(2)在定义域(0,+∞)内任取两个值x1,x2,并规定大小,然后将它们的函数值进行作差比较,确定符号,根据单调性的定义可知该函数的单调性;
(3)根据题意可转化成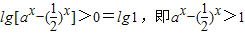 对x∈[1,+∞)恒成立,只需研究
对x∈[1,+∞)恒成立,只需研究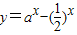 在[1,+∞)上的最小值恒大于1即可.
在[1,+∞)上的最小值恒大于1即可.
解答:解: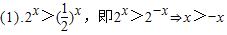 ,
,
∴x>0.f(x)的定义域为(0,+∞)
(2)当a>1时,函数的定义域为(0,+∞).任取0<x1<x2,
则g(x1)-g(x2)=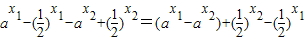 ,
,
由于a>1,有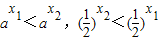 ,
,
∴y1-y2<0,即y1<y2
∴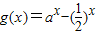 在其定义域上是增函数.(也可:由a>1,知ax递增,0.5x递减,-(0.5)x也递增,故g(x)递增)
在其定义域上是增函数.(也可:由a>1,知ax递增,0.5x递减,-(0.5)x也递增,故g(x)递增)
(3)依题意,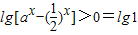 ,即
,即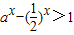 对x∈[1,+∞)恒成立,
对x∈[1,+∞)恒成立,
由于a>1时,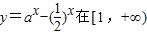 上递增,
上递增,
∴ ,得
,得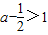 ,∴
,∴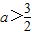 .
.
点评:本题主要考查了函数恒成立问题,以及指数函数的单调性和对数函数的定义域,属于基础题.
(2)在定义域(0,+∞)内任取两个值x1,x2,并规定大小,然后将它们的函数值进行作差比较,确定符号,根据单调性的定义可知该函数的单调性;
(3)根据题意可转化成
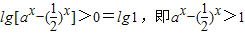 对x∈[1,+∞)恒成立,只需研究
对x∈[1,+∞)恒成立,只需研究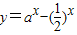 在[1,+∞)上的最小值恒大于1即可.
在[1,+∞)上的最小值恒大于1即可.解答:解:
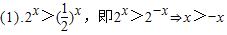 ,
,∴x>0.f(x)的定义域为(0,+∞)
(2)当a>1时,函数的定义域为(0,+∞).任取0<x1<x2,
则g(x1)-g(x2)=
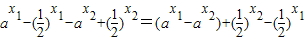 ,
,由于a>1,有
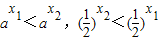 ,
,∴y1-y2<0,即y1<y2
∴
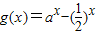 在其定义域上是增函数.(也可:由a>1,知ax递增,0.5x递减,-(0.5)x也递增,故g(x)递增)
在其定义域上是增函数.(也可:由a>1,知ax递增,0.5x递减,-(0.5)x也递增,故g(x)递增)(3)依题意,
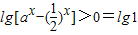 ,即
,即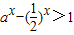 对x∈[1,+∞)恒成立,
对x∈[1,+∞)恒成立,由于a>1时,
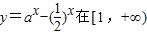 上递增,
上递增,∴
 ,得
,得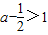 ,∴
,∴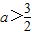 .
.点评:本题主要考查了函数恒成立问题,以及指数函数的单调性和对数函数的定义域,属于基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
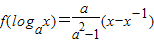 ,其中a>0且a≠1.
,其中a>0且a≠1. ,其中a>0.
,其中a>0.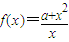 ,(a>0),x∈(0,b),则下列判断正确的是( )
,(a>0),x∈(0,b),则下列判断正确的是( )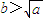 时,f(x)的最小值为
时,f(x)的最小值为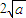
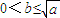 时,f(x)的最小值为
时,f(x)的最小值为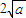
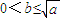 时,f(x)的最小值为
时,f(x)的最小值为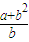
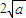
 +bx(a>0)且f′(1)=0,
+bx(a>0)且f′(1)=0,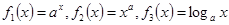 (其中a>0,且a≠),在同一坐标系中画出其中两个函数在第一象限内的图像,其中正确的是
(其中a>0,且a≠),在同一坐标系中画出其中两个函数在第一象限内的图像,其中正确的是