题目内容
已知函数
（1）由
，
，
，
这几个函数值，你能发现f（x）与
有什么关系？并证明你的结论；（2）求
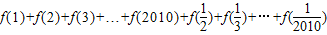的值；（3）判断函数
在区间（0，+∞）上的单调性．
【答案】分析：（1）通过观察这几个函数值，发现f（x）+f（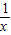
）=1，由函数f（x）的解析式可得到证明；
（2）利用（1）中的结论将自变量互为的两个函数值相加即可救是答案；
（3）利用函数单调性的定义进行证明即可，先设0＜x1＜x2由0＜x1＜x2知x1-x2＜0最后证得：f（x1）＜f（x2）从而
函数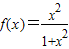
在区间（0，+∞）上为增函数．
解答：解：（1）f（x）+f（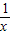
）=（12分）
f（x）+f（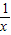
）=
+
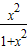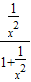=1（5分）
（2）
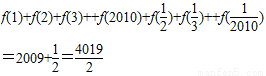（8分）
（3）设0＜x1＜x2
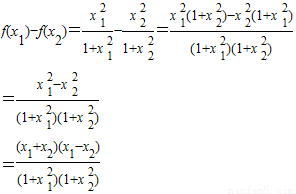（11分）
由0＜x1＜x2知x1-x2＜0（12分）
所以有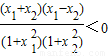
即f（x1）-f（x2）＜0
所以f（x1）＜f（x2）
函数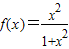
在区间（0，+∞）上为增函数（14分）
点评：本小题主要考查函数单调性的应用、函数的值、归纳推理等基础知识，考查运算求解能力与转化思想．属于中档题．
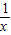）=1，由函数f（x）的解析式可得到证明；（2）利用（1）中的结论将自变量互为的两个函数值相加即可救是答案；
（3）利用函数单调性的定义进行证明即可，先设0＜x1＜x2由0＜x1＜x2知x1-x2＜0最后证得：f（x1）＜f（x2）从而
函数
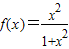在区间（0，+∞）上为增函数．解答：解：（1）f（x）+f（
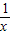）=（12分）f（x）+f（
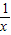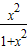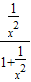）=+=1（5分）（2）
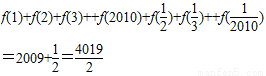（8分）（3）设0＜x1＜x2
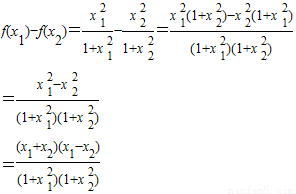（11分）由0＜x1＜x2知x1-x2＜0（12分）
所以有
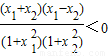即f（x1）-f（x2）＜0所以f（x1）＜f（x2）
函数
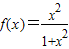在区间（0，+∞）上为增函数（14分）点评：本小题主要考查函数单调性的应用、函数的值、归纳推理等基础知识，考查运算求解能力与转化思想．属于中档题．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
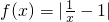
的图象经过怎样的变换可以得到函数y=f（x）的图象？请作出y=f（x）的图象；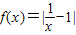
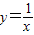的图象经过怎样的变换可以得到函数y=f（x）的图象？请作出y=f（x）的图象；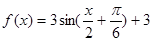
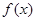的周期、振幅、初相、对称轴；
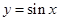上的图象经怎样的变换得到.
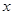的集合；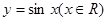
的图象经过怎样的变化而得到的