题目内容
已知函数f(x)=sin sin(
sin(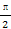 +
+ ).
).
(1)求函数f(x)在[-π,0]上的单调区间.
(2)已知角α满足α∈(0,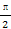 ),2f(2α)+4f(
),2f(2α)+4f(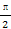 -2α)=1,求f(α)的值.
-2α)=1,求f(α)的值.
 sin(
sin(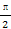 +
+ ).
).(1)求函数f(x)在[-π,0]上的单调区间.
(2)已知角α满足α∈(0,
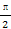 ),2f(2α)+4f(
),2f(2α)+4f(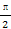 -2α)=1,求f(α)的值.
-2α)=1,求f(α)的值.(1) 单调递减区间为[-π,- ],单调递增区间为[-
],单调递增区间为[- ,0]
,0]
(2)
 ],单调递增区间为[-
],单调递增区间为[- ,0]
,0](2)

【思路点拨】(1)利用诱导公式及倍角公式化简f(x)的解析式后可求.
(2)利用已知将条件代入,整理成单角α的三角函数关系式后可解.
解:f(x)=sin sin(
sin( +
+ )
)
=sin cos
cos =
= sinx.
sinx.
(1)函数f(x)的单调递减区间为[-π,- ],单调递增区间为[-
],单调递增区间为[- ,0].
,0].
(2)2f(2α)+4f( -2α)=1
-2α)=1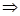 sin2α+2sin(
sin2α+2sin( -2α)=1
-2α)=1
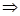 2sinαcosα+2(cos2α-sin2α)=1
2sinαcosα+2(cos2α-sin2α)=1
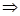 cos2α+2sinαcosα-3sin2α=0
cos2α+2sinαcosα-3sin2α=0
⇒(cosα+3sinα)(cosα-sinα)=0.
∵α∈(0, ),
),
∴cosα-sinα=0⇒tanα=1得α=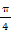 ,故sinα=
,故sinα=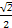 ,
,
∴f(α)= sinα=
sinα= .
.
(2)利用已知将条件代入,整理成单角α的三角函数关系式后可解.
解:f(x)=sin
 sin(
sin( +
+ )
)=sin
 cos
cos =
= sinx.
sinx.(1)函数f(x)的单调递减区间为[-π,-
 ],单调递增区间为[-
],单调递增区间为[- ,0].
,0].(2)2f(2α)+4f(
 -2α)=1
-2α)=1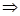 sin2α+2sin(
sin2α+2sin( -2α)=1
-2α)=1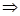 2sinαcosα+2(cos2α-sin2α)=1
2sinαcosα+2(cos2α-sin2α)=1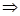 cos2α+2sinαcosα-3sin2α=0
cos2α+2sinαcosα-3sin2α=0⇒(cosα+3sinα)(cosα-sinα)=0.
∵α∈(0,
 ),
),∴cosα-sinα=0⇒tanα=1得α=
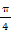 ,故sinα=
,故sinα=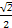 ,
,∴f(α)=
 sinα=
sinα= .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
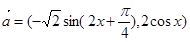 ,
,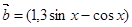 ,
,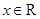 ,函数
,函数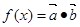 .
.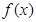 的最小正周期;
的最小正周期;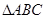 中,角
中,角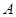 、
、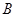 、
、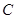 所对的边分别为
所对的边分别为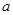 、
、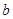 、
、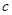 ,
,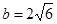 ,
,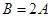 ,
,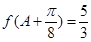 ,求
,求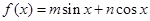 ,且
,且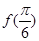 是它的最大值,(其中m、n为常数且
是它的最大值,(其中m、n为常数且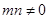 )给出下列命题:①
)给出下列命题:①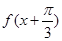 是偶函数;②函数
是偶函数;②函数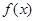 的图象关于点
的图象关于点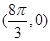 对称;③
对称;③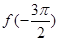 是函数
是函数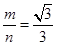 .
.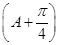 =
=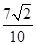 ,A∈
,A∈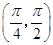 .
.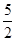 sinAsinx的值域.
sinAsinx的值域. )来表示(x为月份),已知3月份达到最高价9万元,7月份价格最低,为5万元,则国庆节期间的价格约为( )
)来表示(x为月份),已知3月份达到最高价9万元,7月份价格最低,为5万元,则国庆节期间的价格约为( ) sin x,sin x),b=(cos x,sin x),x∈
sin x,sin x),b=(cos x,sin x),x∈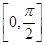 .
.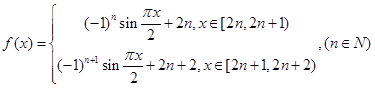 ,若数列
,若数列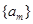 满足
满足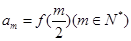 ,且
,且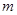 项和为
项和为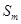 ,则
,则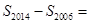 _____________.
_____________. 满足
满足 当
当 时,
时, ,则
,则 ( )
( )


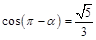 ,且
,且 ,则
,则 ( )
( )


