题目内容
袋中装有若干个质地均匀大小一致的红球和白球,白球数量是红球数量的两倍.每次从袋中摸出一个球然后放回,若累计3次摸到红球则停止摸球,否则继续摸球直至第5次摸球后结束.
(1)求摸球3次就停止的事件发生的概率;
(2)记摸到红球的次数为 ,求随机变量
,求随机变量 的分布列及其期望.
的分布列及其期望.
(1)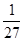 ;
;
(2)随机变量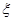 的分布列是
的分布列是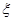
0 1 2 3 P 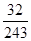
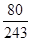
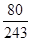
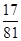
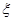 的数学期望为:
的数学期望为: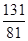
解析试题分析:因为白球数量是红球数量的两倍.每次从袋中摸出一个球然后放回,所以每次摸到红球的概率都是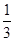 ,摸到白球的概率是
,摸到白球的概率是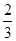 ,摸球3次就停止,说明前三次都摸到红球,相当于三次独立重复试验,摸到红球连续发生三次;
,摸球3次就停止,说明前三次都摸到红球,相当于三次独立重复试验,摸到红球连续发生三次;
(2)根据题意,随机变量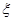 的取值为0,1,2,3,利用独立重复试验的概率公式求出分布列及数学期望.
的取值为0,1,2,3,利用独立重复试验的概率公式求出分布列及数学期望.
试题解析:(1)摸球3次就停止,说明前三次分别都摸到了红球,
则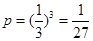 (5分)
(5分)
(2)随机变量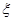 的取值为0,1,2,3.
的取值为0,1,2,3.
则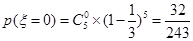 ,
,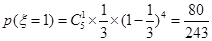
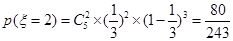 ,
,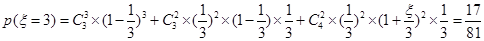 .
.
随机变量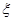 的分布列是
的分布列是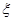
0 1 2 3 P 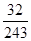
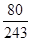
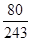
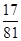
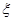 的数学期望为:
的数学期望为: . (12分)
. (12分)
考点:1、古典概型;2、独立重复试验;3、离散型随机变量的分布列与数学期望.

练习册系列答案
相关题目
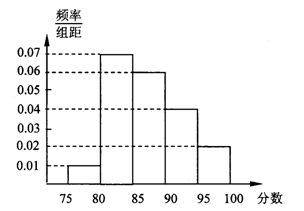
 ,否则其获胜的概率为
,否则其获胜的概率为 .
.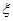 为比赛结束时甲的得分,求随机变量
为比赛结束时甲的得分,求随机变量 .
.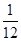 (i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大?
(i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大? 月
月 日至
日至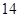 日的空气质量指数趋势图,空气质量指数(
日的空气质量指数趋势图,空气质量指数(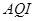 )小于
)小于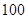 表示空气质量优良,空气质量指数大于
表示空气质量优良,空气质量指数大于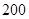 表示空气重度污染,某人随机选择
表示空气重度污染,某人随机选择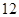 日中的某一天到达该市,并停留
日中的某一天到达该市,并停留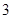 天.
天.
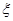 是此人停留期间空气重度污染的天数,求
是此人停留期间空气重度污染的天数,求 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为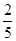 ,中奖可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为X,求X≤3的概率.
,中奖可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为X,求X≤3的概率.