题目内容
△ABC中,角A,B,C的对边分别为a,b,c,且b2+c2-a2+bc=0.
(1)求角A的大小;
(2)若a=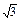 ,求bc的最大值;
,求bc的最大值;
(3)求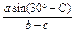 的值.
的值.
(1)求角A的大小;
(2)若a=
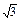 ,求bc的最大值;
,求bc的最大值;(3)求
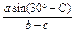 的值.
的值.(1)A=120°(2)bc取得最大值为1(3)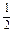
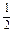
(1)∵cosA=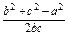 =
=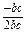 =-
=-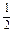 , 2分
, 2分
又∵A∈(0°,180°),∴A=120°. 4分
(2)由a=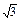 ,得b2+c2=3-bc,
,得b2+c2=3-bc,
又∵b2+c2≥2bc(当且仅当c=b时取等号),
∴3-bc≥2bc(当且仅当c=b时取等号). 6分
即当且仅当c=b=1时,bc取得最大值为1. 8分
(3)由正弦定理得: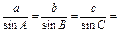 2R,
2R,
∴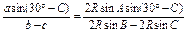 10分
10分
=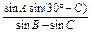 11分
11分
=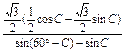 12分
12分
=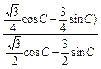 13分
13分
=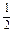 . 14分
. 14分
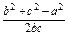 =
=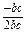 =-
=-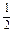 , 2分
, 2分又∵A∈(0°,180°),∴A=120°. 4分
(2)由a=
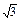 ,得b2+c2=3-bc,
,得b2+c2=3-bc,又∵b2+c2≥2bc(当且仅当c=b时取等号),
∴3-bc≥2bc(当且仅当c=b时取等号). 6分
即当且仅当c=b=1时,bc取得最大值为1. 8分
(3)由正弦定理得:
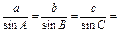 2R,
2R,∴
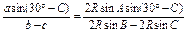 10分
10分=
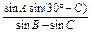 11分
11分=
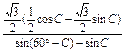 12分
12分=
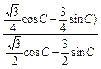 13分
13分=
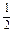 . 14分
. 14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中,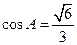 ,
,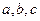 分别是角
分别是角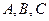 所对的边.
所对的边.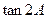 ; (Ⅱ)若
; (Ⅱ)若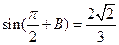 ,
,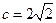 ,求
,求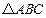 中,
中,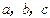 分别是三个内角
分别是三个内角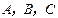 的对边.若
的对边.若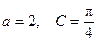 ,
,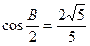 ,
,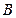 的余弦值;
的余弦值;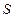 .
.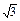 -1)n mile的B处有一艘走私船,在A处北偏西75°的方向,距离A 2 n mile的C处的缉私船奉命以10
-1)n mile的B处有一艘走私船,在A处北偏西75°的方向,距离A 2 n mile的C处的缉私船奉命以10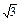 )km.试画出示意图,并计算出从A到D的方位角和距离(结果保留根号).
)km.试画出示意图,并计算出从A到D的方位角和距离(结果保留根号).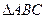 中角A、B、C的对边分别为
中角A、B、C的对边分别为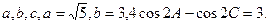
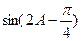 的值。
的值。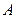 、
、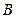 、
、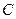 为
为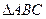 的三内角,且其对边分别为
的三内角,且其对边分别为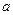 、
、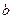 、
、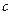 ,若
,若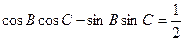 .
.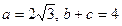 ,求
,求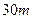 的圆形广场中央上空,设置一个照明光源,射向地面的光呈圆锥形,且其轴截面顶角为
的圆形广场中央上空,设置一个照明光源,射向地面的光呈圆锥形,且其轴截面顶角为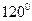 ,若要光源恰好照亮整个广场,则其高应为_______
,若要光源恰好照亮整个广场,则其高应为_______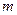 (精确到
(精确到 )
)