题目内容
已知,如图,AB是圆柱的母线,BC是圆柱底面圆的直径,D是圆柱底面圆上与B、C不重合的点,用<MN,EF>表示直线MN、EF的夹角.
(Ⅰ)在三棱锥A-BCD中,写出所有两棱的夹角(不写出具体的角度值);
(Ⅱ)在三棱锥A-BCD中的六条棱中取两条棱,求这两条棱互相垂直的概率.

(Ⅰ)在三棱锥A-BCD中,写出所有两棱的夹角(不写出具体的角度值);
(Ⅱ)在三棱锥A-BCD中的六条棱中取两条棱,求这两条棱互相垂直的概率.

(Ⅰ)由题意可得<AD,AB>,<AB,AC>,<AC,AD>,<AB,CD>,<AB,BC>,
<AB,BD>,<AC,BC>,<AC,BD>,<AC,CD>,<AD,BD>,
<AD,CD>,<AD,BC>,<BC,BD>,<BC,CD>,<BD,CD>.
共15个;
(Ⅱ)∵AB是圆柱的母线,∴<AB,BC>=
,<AB,BD>=
,<AB,CD>=
.
∵BC是圆柱底面圆的直径,∴<BD,CD>=
,∴CD⊥平面ABD,∴CD⊥AD.
设“在三棱锥A-BCD中的六条棱中取两条棱,这两条棱互相垂直”为事件E,则P(E)=
=
.
∴在三棱锥A-BCD中的六条棱中取两条棱,这两条棱互相垂直的概率为
.
<AB,BD>,<AC,BC>,<AC,BD>,<AC,CD>,<AD,BD>,
<AD,CD>,<AD,BC>,<BC,BD>,<BC,CD>,<BD,CD>.
共15个;
(Ⅱ)∵AB是圆柱的母线,∴<AB,BC>=
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∵BC是圆柱底面圆的直径,∴<BD,CD>=
| π |
| 2 |
设“在三棱锥A-BCD中的六条棱中取两条棱,这两条棱互相垂直”为事件E,则P(E)=
| 5 |
| 15 |
| 1 |
| 3 |
∴在三棱锥A-BCD中的六条棱中取两条棱,这两条棱互相垂直的概率为
| 1 |
| 3 |

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
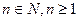 )次后,将所得的正方体随机地拿出一个,则恰好拿到三个面都涂有颜色的小正方体的概率是( )
)次后,将所得的正方体随机地拿出一个,则恰好拿到三个面都涂有颜色的小正方体的概率是( )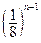
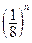
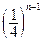
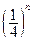
 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率 .
.  ;
; :“取出的2件产品中至少有一件二等品”的概率
:“取出的2件产品中至少有一件二等品”的概率 .
.