题目内容
设数列{an}的前n项的和为Sn,已知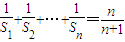 ,设
,设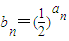 若对一切n∈N*均有
若对一切n∈N*均有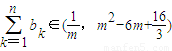 ,则实数m的取值范围为 .
,则实数m的取值范围为 .
【答案】分析:依题意,可求得an与bn,从而可求得 bk=
bk=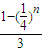 ∈[
∈[ ,
, ),利用[
),利用[ ,
, )⊆(
)⊆(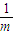 ,m2-6m+
,m2-6m+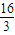 )即可求得实数m的取值范围.
)即可求得实数m的取值范围.
解答:解:∵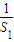 +
+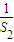 +…+
+…+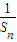 =
=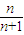 ,①
,①
∴当n≥2时,
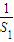 +
+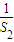 +…+
+…+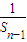 =
=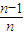 ,②
,②
∴①-②得: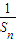 =
=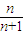 -
-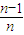 =
=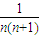 ,
,
∴Sn=n(n+1)(n≥2).
当n=1时,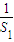 =
=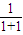 =
= ,
,
∴a1=2,符合Sn=n(n+1)(n≥2).
∴Sn=n(n+1).
∴可求得an=2n.
∴bn=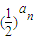 =
=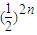 =
=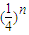 .
.
∵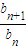 =
= ,b1=
,b1= ,
,
∴{bn}是以 为首项,
为首项, 为公比的等比数列.
为公比的等比数列.
∴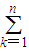 bk=
bk=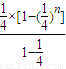 =
=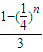 ∈[
∈[ ,
, ),
),
∵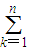 bk∈(
bk∈(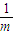 ,m2-6m+
,m2-6m+ ),
),
∴[ ,
, )⊆(
)⊆(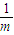 ,m2-6m+
,m2-6m+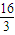 ),
),
即 ,
,
解得:m<0或m≥5.
故答案为:m<0或m≥5.
点评:本题考查求数列的通项与数列求和,突出考查集合间的包含关系与解不等式组的能力,综合性强,难度大,属于难题.
 bk=
bk=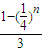 ∈[
∈[ ,
, ),利用[
),利用[ ,
, )⊆(
)⊆(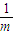 ,m2-6m+
,m2-6m+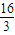 )即可求得实数m的取值范围.
)即可求得实数m的取值范围.解答:解:∵
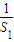 +
+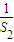 +…+
+…+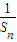 =
=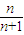 ,①
,①∴当n≥2时,
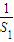 +
+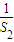 +…+
+…+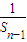 =
=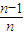 ,②
,②∴①-②得:
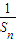 =
=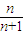 -
-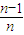 =
=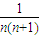 ,
,∴Sn=n(n+1)(n≥2).
当n=1时,
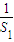 =
=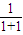 =
= ,
,∴a1=2,符合Sn=n(n+1)(n≥2).
∴Sn=n(n+1).
∴可求得an=2n.
∴bn=
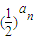 =
=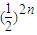 =
=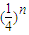 .
.∵
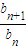 =
= ,b1=
,b1= ,
,∴{bn}是以
 为首项,
为首项, 为公比的等比数列.
为公比的等比数列.∴
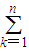 bk=
bk=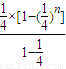 =
=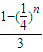 ∈[
∈[ ,
, ),
),∵
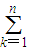 bk∈(
bk∈(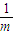 ,m2-6m+
,m2-6m+ ),
),∴[
 ,
, )⊆(
)⊆(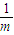 ,m2-6m+
,m2-6m+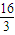 ),
),即
 ,
,解得:m<0或m≥5.
故答案为:m<0或m≥5.
点评:本题考查求数列的通项与数列求和,突出考查集合间的包含关系与解不等式组的能力,综合性强,难度大,属于难题.

练习册系列答案
相关题目