题目内容
18.已知函数f(x)的定义域为R,且满足f(x+2)=-f(x).(1)求证:f(x)是周期函数;
(2)若f(x)为奇函数,且当0≤x≤1时,f(x)=$\frac{1}{2}$x,求使f(x)=-$\frac{1}{2}$在[0,2009]上的所有x的个数.
分析 (1)根据函数周期性的定义即可证明f(x)是周期函数;
(2)根据函数的奇偶性和周期性的关系求出函数f(x)在一个周期内的图象,作出函数f(x)和y=-$\frac{1}{2}$的图象,观察两个图象在一个周期内的交点个数即可得到结论.
解答 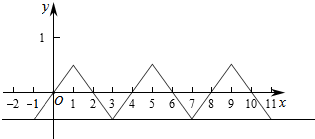 证明:(1)∵f(x+2)=-f(x).
证明:(1)∵f(x+2)=-f(x).
∴f(x+4)=-f(x+2)=f(x).
故函数是周期为4的周期函数.
解:(2)若-1≤x≤0,则0≤-x≤1,
则f(-x)=-$\frac{1}{2}$x,
∵f(x)为奇函数,
∴f(-x)=-$\frac{1}{2}$x=-f(x),
即f(x)=$\frac{1}{2}$x,-1≤x≤0,
即f(x)=$\frac{1}{2}$x,-1≤x≤1,
若1≤x≤3,则-1≤x-2≤1,
∵f(x+2)=-f(x).
∴f(x)=-f(x-2).
即当1≤x≤3时,f(x)=-f(x-2)=-$\frac{1}{2}$(x-2).
作出函数f(x)在一个周期上的图象如图:
若f(x)=-$\frac{1}{2}$,在在一个周期[0,4]内只有一个根x=3,
∵2009=4×502+1,
∴在[0,2009]上共有502个周期,
∴使f(x)=-$\frac{1}{2}$在[0,2009]上的所有x的个数为502.
点评 本题主要考查函数周期性的判断,以及函数交点个数的求解,利用函数奇偶性和周期性的关系,求出函数的解析式,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
8.盒子里共有大小相同的3只白球,1只黑球.若从中随机摸出两只球,则它们颜色不同的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
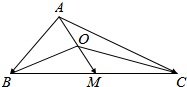 如图,在△ABC中,O为中线AM上的动点.
如图,在△ABC中,O为中线AM上的动点.