题目内容
【题目】半圆![]() 的直径的两端点为
的直径的两端点为![]() ,点
,点![]() 在半圆
在半圆![]() 及直径
及直径![]() 上运动,若将点
上运动,若将点![]() 的纵坐标伸长到原来的2倍(横坐标不变)得到点
的纵坐标伸长到原来的2倍(横坐标不变)得到点![]() ,记点
,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若称封闭曲线上任意两点距离的最大值为该曲线的“直径”,求曲线![]() 的“直径”.
的“直径”.
【答案】(1)答案见解析 (2)![]() .
.
【解析】
(1)设![]() ,则
,则![]() ,由题意可知当
,由题意可知当![]() 在直径
在直径![]() 上时,显然
上时,显然![]() ;当
;当![]() 在半圆
在半圆![]() 上时,
上时, ,即可求得答案;
,即可求得答案;
(2)设曲线![]() 上两动点
上两动点![]() ,显然
,显然![]() ,
,![]() 至少有一点在椭圆上时
至少有一点在椭圆上时![]() 才能取得最大,不妨设
才能取得最大,不妨设![]() ,
,![]() ,根据不等式性质,即可求得曲线
,根据不等式性质,即可求得曲线![]() 的“直径”.
的“直径”.
(1)设![]() ,则
,则![]() ,
,
由题意可知当![]() 在直径
在直径![]() 上时,显然
上时,显然![]() ;
;
当![]() 在半圆
在半圆![]() 上时,
上时, ,
,
![]() 曲线
曲线![]() 的方程为
的方程为![]() 或
或![]() .
.
(2)设曲线![]() 上两动点
上两动点![]() ,
,
显然![]() ,
,![]() 至少有一点在椭圆上时
至少有一点在椭圆上时![]() 才能取得最大,
才能取得最大,
不妨设![]() ,
,
则![]() ,
,
![]()
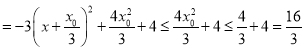
![]()
等号成立时: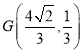 ,
,![]() 或
或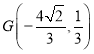 ,
,![]() ,
,
由两点距离公式可得:![]() ,
,
故曲线![]() 的“直径”为
的“直径”为![]() .
.

【题目】某公司为提高市场销售业绩,设计了一套产品促销方案,并在某地区部分营销网点进行试点.运作一年后,对“采取促销”和“没有采取促销”的营销网点各选了50个,对比上一年度的销售情况,分别统计了它们的年销售总额,并按年销售总额增长的百分点分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,分别统计后制成如图所示的频率分布直方图,并规定年销售总额增长10个百分点及以上的营销网点为“精英店”.
,分别统计后制成如图所示的频率分布直方图,并规定年销售总额增长10个百分点及以上的营销网点为“精英店”.
“采用促销”的销售网点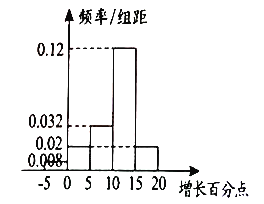
“不采用促销”的销售网点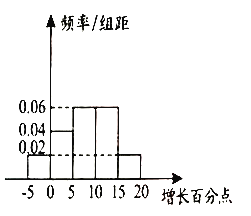
(1)请根据题中信息填充下面的列联表,并判断是否有![]() 的把握认为“精英店与采促销活动有关”;
的把握认为“精英店与采促销活动有关”;
采用促销 | 无促销 | 合计 | |
精英店 | |||
非精英店 | |||
合计 | 50 | 50 | 100 |
(2)某“精英店”为了创造更大的利润,通过分析上一年度的售价![]() (单位:元)和日销量
(单位:元)和日销量![]() (单位:件)(
(单位:件)(![]() )的一组数据后决定选择
)的一组数据后决定选择![]() 作为回归模型进行拟合.具体数据如下表,表中的
作为回归模型进行拟合.具体数据如下表,表中的![]()
|
|
|
|
|
|
|
45.8 | 395.5 | 2413.5 | 4.6 | 21.6 |
|
|
①根据上表数据计算![]() ,
,![]() 的值;
的值;
②已知该公司产品的成本为10元/件,促销费用平均5元/件,根据所求出的回归模型,分析售价![]() 定为多少时日利润
定为多少时日利润![]() 可以达到最大.
可以达到最大.
附①: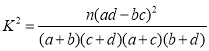
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
附②:对应一组数据![]() ,
,
其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为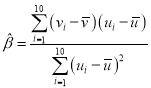 ,
,![]() .
.