Question

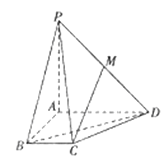
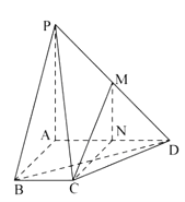
【题目】如图，四棱锥中，底面，，为的中点

（1）证明：平面

（2）若是边长为2的等边三角形，求二面角的余弦值

Answer 1

【答案】（1）证明见解析 （2）

【解析】

（1）取中点，得到，从而平面，可得到四边形是平行四边形，得到，从而平面，得到平面平面，从而证明平面；（2）建立空间直角坐标系，得到平面的法向量和平面的法向量，利用向量夹角公式，得到二面角的余弦值.

（1）如图取中点，连接和，

为的中点，，

平面，平面

平面，

，

又，

四边形是平行四边形，，

平面，平面

平面

又因为，平面，平面，

平面平面，

而平面

平面；

（2）根据题意，建立空间直角坐标系，

为等边三角形，，不妨设，

则，，

设平面的法向量，

由，得，

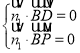令，得，

平面PAB，

平面的法向量

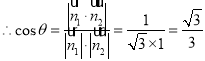
二面角A-PB-M的余弦值为