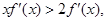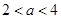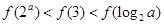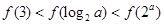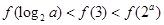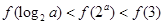题目内容
已知函数 的导函数
的导函数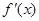 满足
满足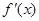 >
> (
( ),则( )
),则( )
A. > >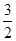 | B. < <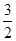 |
C. > >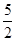 | D. < <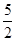 |
A
解析试题分析:构造函数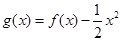 ,则
,则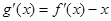
∵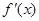 >
> , ∴
, ∴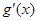 >0, ∴
>0, ∴ 在R上递增, ∴
在R上递增, ∴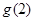 >
>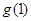
即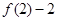 >
>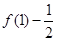 ,∴
,∴ >
>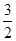 ,故选A.
,故选A.
考点:导数计算,利用导数研究函数的单调性。
点评:中档题,在某区间,导数值非负,函数为增函数,导数值非正,函数为减函数。解答本题关键是构造函数。

练习册系列答案
相关题目
设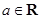 ,函数
,函数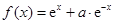 的导函数是
的导函数是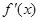 ,且
,且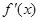 是奇函数.若曲线
是奇函数.若曲线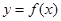 的一条切线的斜率是
的一条切线的斜率是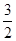 ,则切点的横坐标为( )
,则切点的横坐标为( )
A.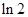 | B.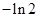 | C.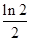 | D.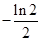 |
函数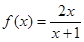 在[1,2]的最大值和最小值分别是 ( )
在[1,2]的最大值和最小值分别是 ( )
A.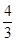 ,1 ,1 | B.1,0 | C.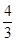 , ,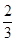 | D.1,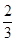 |
设函数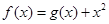 ,曲线
,曲线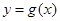 在点
在点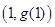 处的切线方程为
处的切线方程为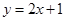 ,则曲线
,则曲线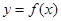 在点
在点 处切线的斜率为
处切线的斜率为
| A.4 | B.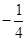 | C. | D.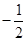 |
若曲线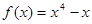 在点P处的切线平行于直线
在点P处的切线平行于直线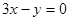 ,则点P的坐标为 ( )
,则点P的坐标为 ( )
| A.(1,0) | B.(1,5) | C.(1,-3) | D.(-1,2) |
已知函数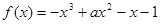 在
在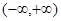 上是单调函数,则实数a的取值范围是( )
上是单调函数,则实数a的取值范围是( )
A.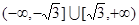 | B.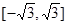 |
C.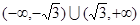 | D.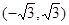 |
若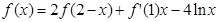 ,则
,则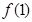 等于( )
等于( )
A.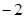 | B.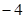 | C.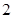 | D.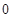 |
若曲线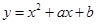 在点
在点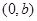 处的切线方程是
处的切线方程是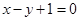 ,则( )
,则( )
A.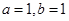 | B.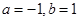 |
C.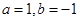 | D.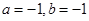 |
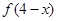
 ,且当
,且当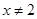
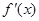 满足
满足