题目内容
设a,b为实数,我们称(a,b)为有序实数对.类似地,设A,B,C为集合,我们称(A,B,C)为有序三元组.如果集合A,B,C满足|A∩B|=|B∩C|=|C∩A|=1,且A∩B∩C=∅,则我们称有序三元组(A,B,C)为最小相交(|S|表示集合S中的元素的个数).
(Ⅰ)请写出一个最小相交的有序三元组,并说明理由;
(Ⅱ)由集合{1,2,3,4,5,6}的子集构成的所有有序三元组中,令N为最小相交的有序三元组的个数,求N的值.
解:(Ⅰ)设A={1,2},B={2,3},C={1,3},
则A∩B={2},B∩C={3},C∩A={1},A∩B∩C=∅,且|A∩B|=|B∩C|=|C∩A|=1.
所以(A,B,C)是一个最小相交的有序三元组. …
(Ⅱ)令S={1,2,3,4,5,6},如果(A,B,C)是由S的子集构成的最小相交的有序三元组,
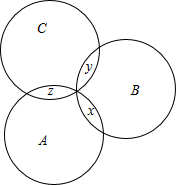
则存在两两不同的x,y,z∈S,使得A∩B={x},B∩C={y},C∩A={z},
(如图),要确定x,y,z共有6×5×4种方法;
对S中剩下的3个元素,每个元素有4种分配方式,
即它属于集合A,B,C中的某一个或不属于任何一个,则有43种确定方法.
所以最小相交的有序三元组(A,B,C)的个数N=6×5×4×43=7680.…
分析:(Ⅰ)设A={1,2},B={2,3},C={1,3},则满足题意,所以(A,B,C)是一个最小相交的有序三元组.
(Ⅱ)令S={1,2,3,4,5,6},由题意知,必存在两两不同的x,y,z∈S,使得A∩B={x},B∩C={y},C∩A={z},
而要确定x,y,z共有6×5×4种方法;对S中剩下的3个元素,每个元素有4种分配方式,即可得到最小相交的有序三元组(A,B,C)的个数N.
点评:此题考查集合的新定义,在新定义下计算集合间的交、并、补运算,这是高考中的常考内容,要认真掌握,并确保得分.
则A∩B={2},B∩C={3},C∩A={1},A∩B∩C=∅,且|A∩B|=|B∩C|=|C∩A|=1.
所以(A,B,C)是一个最小相交的有序三元组. …
(Ⅱ)令S={1,2,3,4,5,6},如果(A,B,C)是由S的子集构成的最小相交的有序三元组,
则存在两两不同的x,y,z∈S,使得A∩B={x},B∩C={y},C∩A={z},
(如图),要确定x,y,z共有6×5×4种方法;

对S中剩下的3个元素,每个元素有4种分配方式,
即它属于集合A,B,C中的某一个或不属于任何一个,则有43种确定方法.
所以最小相交的有序三元组(A,B,C)的个数N=6×5×4×43=7680.…
分析:(Ⅰ)设A={1,2},B={2,3},C={1,3},则满足题意,所以(A,B,C)是一个最小相交的有序三元组.
(Ⅱ)令S={1,2,3,4,5,6},由题意知,必存在两两不同的x,y,z∈S,使得A∩B={x},B∩C={y},C∩A={z},
而要确定x,y,z共有6×5×4种方法;对S中剩下的3个元素,每个元素有4种分配方式,即可得到最小相交的有序三元组(A,B,C)的个数N.
点评:此题考查集合的新定义,在新定义下计算集合间的交、并、补运算,这是高考中的常考内容,要认真掌握,并确保得分.

练习册系列答案
相关题目