题目内容
18.设函数f(x)=x|x-a|,0≤x≤1的最大值是g(a),求g(a)的解析式,并求出g(a)的最小值.分析 根据绝对值的性质把函数表示为分段函数形式,结合一元二次函数的图象和性质进行讨论即可.
解答  解:f(x)=$\left\{\begin{array}{l}{x(x-a),}&{x≥a}\\{x(a-x),}&{x<a}\end{array}\right.$,
解:f(x)=$\left\{\begin{array}{l}{x(x-a),}&{x≥a}\\{x(a-x),}&{x<a}\end{array}\right.$,
若a≤0,则f(x)对应的图象为(1),此时函数在0≤x≤1上为增函数,则此时的最大值为f(x)max=g(a)=g(1)=|1-a|=1-a,
当0<a<1时,f($\frac{a}{2}$)=$\frac{a}{2}$•|$\frac{a}{2}$-a|=$\frac{a}{2}$•|$\frac{a}{2}$|=$\frac{{a}^{2}}{4}$,f(1)=1-a,
则f($\frac{a}{2}$)-f(1)=$\frac{{a}^{2}}{4}$+a-1=$\frac{{a}^{2}+4a-4}{4}$,
①当a2+4a-4>0时,解得a>-2+2$\sqrt{2}$或a<-2-2$\sqrt{2}$,
即-2+2$\sqrt{2}$<a<1时,f($\frac{a}{2}$)-f(1)>0,
则f($\frac{a}{2}$)>f(1),此时最大值为值g(a)=f($\frac{a}{2}$)=$\frac{{a}^{2}}{4}$,
②当a2+4a-4=0时,解得a=-2+2$\sqrt{2}$或a=-2-2$\sqrt{2}$(舍),
即a=-2+2$\sqrt{2}$时,f($\frac{a}{2}$)-f(1)=0,
则f($\frac{a}{2}$)=f(1),此时最大值为值g(a)=f($\frac{a}{2}$)=$\frac{{a}^{2}}{4}$=1-a;
③当a2+4a-4<0时,解得-2-2$\sqrt{2}$<a<-2+2$\sqrt{2}$,
即0<a<-2+2$\sqrt{2}$时,f($\frac{a}{2}$)-f(1)<0,
则f($\frac{a}{2}$)<f(1),此时最大值为值g(a)=f(1)=1-a.
点评 本题主要考查函数的最值的求解,利用绝对值的性质将不等式转化为一元二次函数,利用一元二次函数的性质进行求解是解决本题的关键.综合性较强,难度较大.

 优等生题库系列答案
优等生题库系列答案| A. | f(x)=2x-1•2x+1,g(x)=4x | B. | $f(x)=\sqrt{x^2},g(x)={({\sqrt{x}})^2}$ | ||
| C. | $f(x)=\frac{{{x^2}-2}}{{x-\sqrt{2}}},g(x)=x+\sqrt{2}$ | D. | $f(x)=\sqrt{x+1}•\sqrt{x-1},g(x)=\sqrt{{x^2}-1}$ |
| A. | 不具有线性相关关系 | B. | 具有线性相关关系 | ||
| C. | 它们的线性关系还要进一步确定 | D. | 不确定 |
| A. | f(x)=x${\;}^{\frac{1}{2}}$ | B. | f(x)=3x | C. | f(x)=($\frac{1}{2}$)x | D. | f(x)=log2x |
| A. | x3<y3 | B. | log${\;}_{\frac{1}{3}}$x<log${\;}_{\frac{1}{3}}$y | ||
| C. | ($\frac{1}{3}$)x$<(\frac{1}{3})^{y}$ | D. | $\frac{3}{x}<\frac{3}{y}$ |
| A. | [-2,3] | B. | (1,3] | C. | (1,3) | D. | (1,2] |
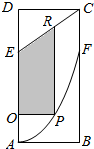 某市政府欲在如图所示的矩形ABCD的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形OPRE(线段EO和RP为两条底边),已知AB=2km,BC=6km,AE=BF=4km,其中曲线AF是以A为顶点、AD为对称轴的抛物线的一部分.
某市政府欲在如图所示的矩形ABCD的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形OPRE(线段EO和RP为两条底边),已知AB=2km,BC=6km,AE=BF=4km,其中曲线AF是以A为顶点、AD为对称轴的抛物线的一部分.