题目内容
设全集U=R,集合A={x∈R|x2-7x+6<0},集合B={x∈R|-1≤x<3}.求A∩B,A∪B,A∩(?UB).
分析:求解一元二次不等式化简集合A,然后直接利用交、并、补集的混合运算求解.
解答:解:由x2-7x+6<0,得1<x<6.
∴A={x∈R|x2-7x+6<0}={x|1<x<6},
又全集U=R,集合B={x∈R|-1≤x<3},
∴A∩B={x|1<x<6}∩{x|-1≤x<3}={x|1<x<3},
A∪B={x|1<x<6}∪{x|-1≤x<3}={x|-1≤x<6},

A∩(?UB)={x|1<x<6}∩{x|x<-1或x≥3}={x|3≤x<6}.
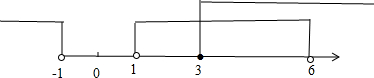
∴A={x∈R|x2-7x+6<0}={x|1<x<6},
又全集U=R,集合B={x∈R|-1≤x<3},
∴A∩B={x|1<x<6}∩{x|-1≤x<3}={x|1<x<3},
A∪B={x|1<x<6}∪{x|-1≤x<3}={x|-1≤x<6},

A∩(?UB)={x|1<x<6}∩{x|x<-1或x≥3}={x|3≤x<6}.

点评:本题考查了交、并、补集的混合运算,考查了一元二次不等式的解法,是基础的计算题.

练习册系列答案
相关题目