题目内容
设 是△
是△ 内一点,且
内一点,且 ,
, ,定义
,定义 ,其中
,其中 、
、 、
、 分别是△
分别是△ 、△
、△ 、△
、△ 的面积,若
的面积,若 , 则
, 则 的最小值是( )
的最小值是( )
 是△
是△ 内一点,且
内一点,且 ,
, ,定义
,定义 ,其中
,其中 、
、 、
、 分别是△
分别是△ 、△
、△ 、△
、△ 的面积,若
的面积,若 , 则
, 则 的最小值是( )
的最小值是( )| A.8 | B.9 | C. 16 | D.18 |
D
试题分析:因为
 ,
, ,所以
,所以 ,
,所以
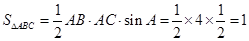 ,因为
,因为 ,所以
,所以
所以
 即
即 的最小值为
的最小值为
点评:求解本题的关键是根据题意得出
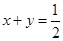 ,然后利用“1”的整体代换和基本不等式求最值,“1”的整体代换可以简化计算,这种方法经常用到,要多加注意,多多练习.
,然后利用“1”的整体代换和基本不等式求最值,“1”的整体代换可以简化计算,这种方法经常用到,要多加注意,多多练习.
练习册系列答案
相关题目
 为锐角三角形,则
为锐角三角形,则

 与
与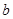 的大小关系为( )。
的大小关系为( )。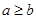



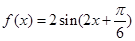 。
。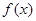 的振幅和最小正周期;
的振幅和最小正周期;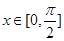 时,函数
时,函数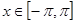 时,求
时,求 ,
, ,则
,则 的终边在( )
的终边在( )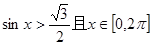 ,则满足题意的
,则满足题意的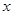 的集合是( )
的集合是( ) 



 ,则
,则 ( )
( )



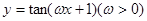 的最小正周期为
的最小正周期为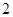 ,则
,则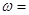 .
.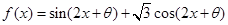 为奇函数,且在
为奇函数,且在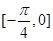 上为减函数的
上为减函数的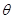 值可以是
值可以是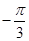
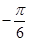
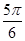
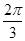
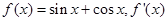 是
是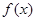 的导函数.
的导函数.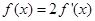 ,求
,求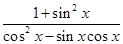 的值.
的值. 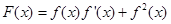 (
(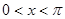 )的单调增区间。
)的单调增区间。