题目内容
如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m.经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),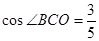 .以
.以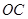 所在直线为
所在直线为 轴,以
轴,以 所在直线为
所在直线为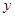 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(Ⅰ)求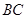 所在直线的方程及新桥BC的长;
所在直线的方程及新桥BC的长;
(Ⅱ)当OM多长时,圆形保护区的面积最大?
并求此时圆的方程.
(1)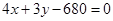 ,
,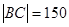 ;(2)线段
;(2)线段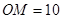 米时,圆形保护区最大;方程为
米时,圆形保护区最大;方程为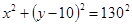
解析试题分析:(1)在求直线方程时,应先选择恰当的直线方程的形式,并注意各种形式的适用条件,用斜截式及点斜式时,直线的斜率必须存在,而两点式不能表示与坐标轴垂直的直线,截距式不能表示与坐标轴垂直的直线或经过原点的直线,故在解题时,若采用截距式,应注意分类讨论,判断截距是否为零;若采用点斜式,应先考虑斜率不存在的情况;(2)根据圆的圆心坐标和半径求圆的标准方程.(3)判断直线与圆的位置关系时,若两方程已知或圆心到直线的距离易表达,用几何法;若方程中含参数,或圆心到直线的距离的表达较繁琐,则用代数法.
试题解析:(Ⅰ)建立平面直角坐标系xOy.
由条件知A(0, 60),C(170, 0),
直线BC的斜率k BC=-tan∠BCO=-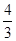 .
.
又因为AB⊥BC,所以直线AB的斜率k AB=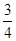
设点B的坐标为(a,b),则k BC=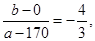
k AB=
解得a=80,b=120.所以BC=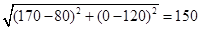 .
.
因此直线BC的方程为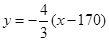 ,即
,即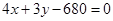 ..............6分
..............6分
新桥BC的长是150 m.
(Ⅱ)设保护区的边界圆M的半径为r m,OM="d" m,(0≤d≤60).
由知,直线BC的方程为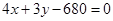
由于圆M与直线BC相切,故点M(0,d)到直线BC的距离是r,
即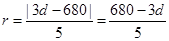 .
.
因为O和A到圆M上任意一点的距离均不少于80 m,
所以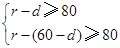 即
即 解得
解得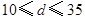
故当d=10时,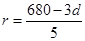 最大,即圆面积最大.
最大,即圆面积最大.
所以当OM =" 10" m时,圆形保护区的面积最大.此时圆的方程为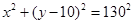 ..........................13分
..........................13分
考点:(1)直线方程的应用;(2)直线与圆的方程的综合应用.

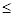 4)的圆心为C,直线L: y=x+m。
4)的圆心为C,直线L: y=x+m。 的最大值;
的最大值;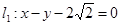 相切
相切 被圆C所截得的弦AB的长.
被圆C所截得的弦AB的长. 过点
过点 ,
,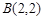 ,并且直线
,并且直线 平分圆的面积.
平分圆的面积.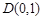 ,且斜率为
,且斜率为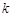 的直线
的直线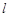 与圆
与圆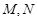 .
.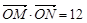 ,求
,求 ,半径小于5.
,半径小于5.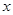 轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为
轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为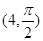 ,若直线l经过点P,且倾斜角为
,若直线l经过点P,且倾斜角为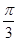 ,圆C的半径为4.
,圆C的半径为4.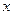 轴上,且与直线
轴上,且与直线 切于(1,1)点的圆的方程为 。
切于(1,1)点的圆的方程为 。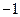 )为圆心且与直线
)为圆心且与直线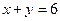 相切的圆
相切的圆 的方程是 .
的方程是 .