题目内容
(本小题满分13分)
已知椭圆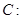
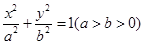 的离心率为
的离心率为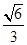 ,椭圆短轴长为
,椭圆短轴长为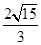 .
.
(Ⅰ)求椭圆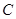 的方程;
的方程;
(Ⅱ)已知动直线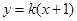 与椭圆
与椭圆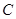 相交于
相交于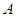 、
、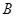 两点. ①若线段
两点. ①若线段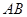 中点的横坐标为
中点的横坐标为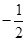 ,求斜率
,求斜率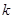 的值;②若点
的值;②若点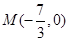 ,求证:
,求证: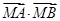 为定值。
为定值。
(Ⅰ)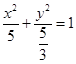 (Ⅱ)①
(Ⅱ)①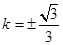 ②
②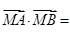
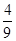
解析试题分析:(Ⅰ)因为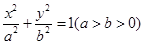 满足
满足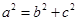 ,
,
。解得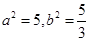 ,则椭圆方程为
,则椭圆方程为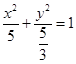 ┄┄┄┄┄┄┄┄┄┄┄┄┄┄4分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄4分
(Ⅱ)(1)将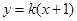 代入
代入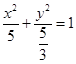 中得
中得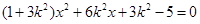
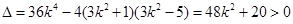
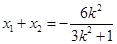
因为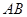 中点的横坐标为
中点的横坐标为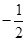 ,所以
,所以 ,解得
,解得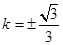 ┄┄┄┄8分
┄┄┄┄8分
(2)由(1)知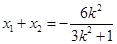 ,
,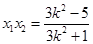
所以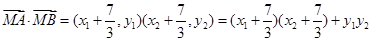
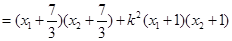
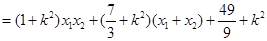
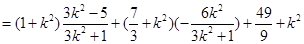 ;┄┄┄┄┄┄┄┄┄11分
;┄┄┄┄┄┄┄┄┄11分
=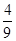 ┄┄┄┄┄┄┄┄┄┄┄┄┄┄13分
┄┄┄┄┄┄┄┄┄┄┄┄┄┄13分
考点:本题考查了椭圆方程的求法及直线与椭圆的位置关系
点评:圆锥曲线是历年高考中比较常见的压轴题之一,近年高考中其解答难度有逐渐降低的趋势,通过解析几何的自身特点,结合相应的数学知识,比如不等式、数列、函数、向量、导数等加以综合。这就要求在分析、解决问题时要充分利用数形结合、设而不求法、弦长公式及韦达定理综合思考,重视函数与方程思想、数形结合思想、对称思想、等价转化思想的应用。

练习册系列答案
相关题目
 为椭圆
为椭圆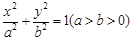 上的一个动点,弦
上的一个动点,弦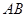 、
、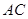 分别过焦点
分别过焦点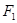 、
、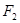 ,当
,当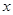 轴时,恰好有
轴时,恰好有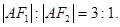
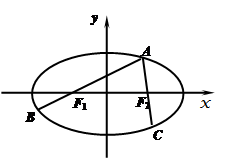
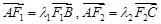 .
.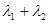 的值;
的值;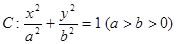 过点
过点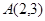 ,且离心率
,且离心率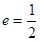 .
.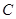 的标准方程;
的标准方程;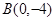 的直线
的直线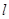 交椭圆于不同的两点M、N,且满足
交椭圆于不同的两点M、N,且满足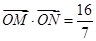 (其中点O为坐标原点),若存在,求出直线
(其中点O为坐标原点),若存在,求出直线 的中心为直角坐标系
的中心为直角坐标系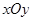 的原点,焦点在
的原点,焦点在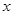 轴上,它的一个顶点到两个焦点的距离分别是7和1
轴上,它的一个顶点到两个焦点的距离分别是7和1 为椭圆
为椭圆 为过
为过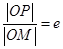 (e为椭圆C的离心率),求点
(e为椭圆C的离心率),求点 中,点
中,点 与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于
与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于 .
.
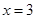 交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由。
交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由。 :
: 的一个顶点为
的一个顶点为 ,离心率为
,离心率为 .直线
.直线 与椭圆
与椭圆 时,求
时,求 的值.
的值. 作直线
作直线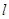 与抛物线
与抛物线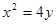 相交于两点
相交于两点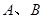 ,圆
,圆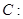
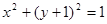
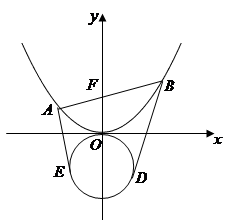
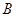 处的切线恰好与圆
处的切线恰好与圆 相切,求直线
相切,求直线 ,
,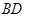 试求
试求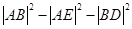 的取值范围.
的取值范围.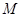 经过定点
经过定点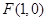 ,且与直线
,且与直线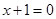 相切。
相切。 方程;
方程;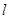 过定点
过定点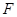 与曲线
与曲线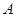 、
、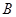 两点:
两点: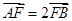 ,求直线
,求直线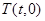 始终在以
始终在以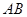 为直径的圆内,求
为直径的圆内,求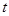 的取值范围。
的取值范围。 的双曲线的方程.
的双曲线的方程.