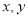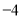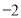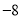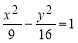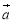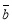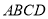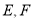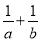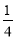题目内容
已知函数y=x-1,令x=―4,―3,―2,-1,0,1,2,3,4,可得函数图象上的九个点,在这九个点中随机取出两个点P1(x1,y1),P2(x2,y2),
(1)求P1,P2两点在双曲线xy=6上的概率;
(2)求P1,P2两点不在同一双曲线xy=k(k≠0)上的概率。
(1)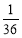 ;(2)
;(2)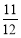 .
.
【解析】
试题分析:(1)写出这9个点的坐标,计算从九个点中选2个点的选法数;从中找出满足方程xy=6的点的个数,计算从中选2个点的选法数,代人古典概型概率公式计算;
(2)两点在同一双曲线xy=k(k≠0)上的有(-3,-4)和(4,3);(-2,-3)和(3,2);(-1,-2)和(2,1)共3对,代人古典概型概率公式计算.
试题解析:(1)函数图象上的九个点分别是:(―4,―5),(―3,―4),(―2,―3),
(―1,―2),(0,―1),(1,0),(2,1),(3,2),(4,3) 2分
从九个点中选2个点共有36种,其中在双曲线xy=6上 4分
设有:(―2,―3),(3,2),故:P1=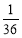 6分
6分
(2)P1,P2在同一双曲线xy=k(k≠0)的有(―3,―4)和(4,3);(―2,―3)和(3,2);
(―1,―2)和(2,1) 9分
故:P2=1-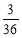 =
=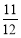 12分.
12分.
考点:古典概型及其概率计算公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目