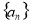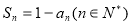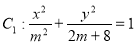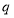题目内容
已知函数f(x)=-x3+ax2-4在x=2处取得极值,若m,n∈[-1,1],则f(m)+f'(n)的最小值为( )
A.-13 B.-15 C.10 D.15
A
【解析】
试题分析:∵f′(x)=-3x2+2ax函数f(x)=-x3+ax2-4在x=2处取得极值∴-12+4a=0
解得a=3∴f′(x)=-3x2+6x∴n∈[-1,1]时,f′(n)=-3n2+6n当n=-1时,f′(n)最小,最小为-9当m∈[-1,1]时,f(m)=-m3+3m2-4,f′(m)=-3m2+6m
令f′(m)=0得m=0,m=2所以m=0时,f(m)最小为-4,故f(m)+f′(n)的最小值为-9+(-4)=-13,故选A.
考点:函数的极值与最值.

练习册系列答案
相关题目