题目内容

已知f（x）=（
1
3
）x-log2x，实数a、b、c满足f（a）f（b）f（c）＜0，（0＜a＜b＜c）若实数x0是方程f（x）=0的一个解，那么下列不等式中，不可能成立的是（　　）
A．x0＜aB．x0＞bC．x0＜cD．x0＞c

精英家教网
因为f（x）=（
1
3
）x-log2x，在定义域上是减函数，
所以0＜a＜b＜c时，f（a）＞f（b）＞f（c）
又因为f（a）f（b）f（c）＜0，
所以一种情况是f（a），f（b），f（c）都为负值，①，
另一种情况是f（a）＞0，f（b）＞0，f（c）＜0．②
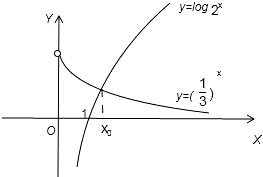
在同一坐标系内画函数y=（
1
3
）x与y=log2x的图象如下，
对于①要求a，b，c都大于x0，
对于②要求a，b都小于x0是，c大于x0．
两种情况综合可得x0＞c不可能成立
故选D．
练习册系列答案
相关题目
已知f（x）=|log3x|，则下列不等式成立的是（　　）
A、f(
1
2
)＞f(2)
B、f(
1
3
)＞f(3)
C、f(
1
4
)＞f(
1
3
)
D、f（2）＞f（3）
13、已知f（x）=log3x+2（x∈[1，9]），则函数y=[f（x）]2+f（x2）的最大值是
13
．
已知f（x）=3mx2-2（m+n）x+n（m≠0）满足f（0）•f（1）＞0，设x1，x2是方程f（x）=0的两根，则|x1-x2|的取值范围为（　　）
A、[
3
3
，
2
3
)
B、[
1
3
，
4
9
)
C、[
1
3
，
3
3
)
D、[
1
9
，
1
3
)
已知f（x）是R上的增函数，且函数f（x）的部分对应值如下表：
x -1 0 1 2 3 4
f（x） -2 -1 -
1
3
1
2
 1 2
则-1＜f（x+1）＜1的解集是（　　）
（2012•江西模拟）已知f（x）=log2x-（
1
3
）x，x0为其零点，且f（a）•f（b）•f（c）＜0，0＜a＜b＜c，则不可能有（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网