题目内容
(10分) 解不等式|x-2|+|x-3|<9
当x≥3时,原不等式为x-2+x-3<9,解得x<7,即有3≤x<7;当2≤x<3时,为x-2+3-x<9,即1<9成立,即有2≤x<3;当x<2时,为2-x+3-x<9,解得x>-2,即有-2<x<2.
综合得原不等式的解集为{x|3≤x<7}∪{x|2≤x<3}∪{x|-2<x<2}={x|-2<x<7}.
综合得原不等式的解集为{x|3≤x<7}∪{x|2≤x<3}∪{x|-2<x<2}={x|-2<x<7}.
解绝对值不等式要采用零点分段法先去绝对值,转化为不等式组来求解.本小题要分三段进行求解,然后再求并集即可.

练习册系列答案
相关题目
 使得不等式
使得不等式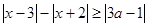 成立,则实数
成立,则实数 的取值范围是 .
的取值范围是 . 恒成立,求实数x
恒成立,求实数x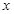 ,不等式
,不等式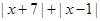 ≥m恒成立.求m的取值范围;
≥m恒成立.求m的取值范围;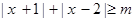 的解集是
的解集是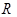
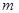 的取值集合M;
的取值集合M;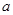 ,
,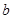 ∈M,试比较
∈M,试比较 与
与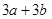 的大小
的大小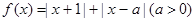 .
.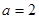 时作出函数
时作出函数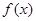 的图象;
的图象;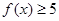 的解集为
的解集为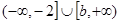 ,求
,求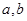 值.
值.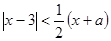 有解,则
有解,则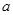 的取值范围是 .
的取值范围是 .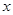 、
、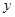 、
、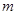 满足
满足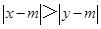 ,则称
,则称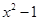 比1远离0,则
比1远离0,则 不等式
不等式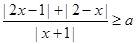 恒成立,则实数
恒成立,则实数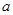 的取值范围是 。
的取值范围是 。