题目内容
【题目】已知![]() ,函数
,函数![]() .
.
(1)求证:曲线![]() 在点
在点![]() 处的切线过定点;
处的切线过定点;
(2)若![]() 是
是![]() 在区间
在区间![]() 上的极大值,但不是最大值,求实数
上的极大值,但不是最大值,求实数![]() 的取值范围;
的取值范围;
(3)求证:对任意给定的正数![]() ,总存在
,总存在![]() ,使得
,使得![]() 在
在![]() 上为单调函数.
上为单调函数.
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:(1)求出切点坐标及切线方程,切线恒过定点即与参数![]() 无关,令系数为
无关,令系数为![]() ,可得定点坐标;(2)
,可得定点坐标;(2)![]() ,要使
,要使![]() 成为极大值,因此
成为极大值,因此![]() ,又
,又![]() 不是最大值,而
不是最大值,而![]() 在
在![]() 单增,
单增,![]() 单减,
单减,![]() 单增,因此
单增,因此![]() ,可求得
,可求得![]() 的范围;(3)
的范围;(3)![]() 在
在![]() 单增,
单增,![]() 单减,
单减,![]() 单增,又
单增,又![]() ,所以要使
,所以要使![]() 在
在![]() 单调,只需
单调,只需![]() ,即
,即![]() ,故存在.
,故存在.
试题解析:解:(1)证明:∵![]() ,∴
,∴![]()
∵![]() ,∴曲线
,∴曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() ,令
,令![]() ,则
,则![]() ,
,
故曲线![]() 在点
在点![]() 处的切线过定点
处的切线过定点![]()
(2)解: ![]() ,
,
令![]() 得
得![]() 或
或![]()
∵![]() 是
是![]() 在区间
在区间![]() 上的极大值,∴
上的极大值,∴![]() ,∴
,∴![]()
令![]() ,得
,得![]() 或
或![]() 递增;令
递增;令![]() ,得
,得![]() 递减,
递减,
∵![]() 不是
不是![]() 在区间
在区间![]() 上的最大值,
上的最大值,
∴![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,
,
∴![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]()
(3)证明: ![]() ,
,
∵![]() ,∴
,∴![]()
令![]() ,得
,得![]() 或
或![]() 递增;令
递增;令![]() ,得
,得![]() 递减,
递减,
∵![]() ,∴
,∴![]()
若![]() 在
在![]() 上为单调函数,则
上为单调函数,则![]() ,即
,即![]()
故对任意给定的正数![]() ,总存在
,总存在![]() (其中
(其中![]() ),使得
),使得![]() 在
在![]() 上为单调函数
上为单调函数

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
【题目】“真人秀”热潮在我国愈演愈烈,为了了解学生是否喜欢某“真人秀”节目,在某中学随机调查了110名学生,得到如下列联表:
男 | 女 | 总计 | |
喜欢 | 40 | 20 | 60 |
不喜欢 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由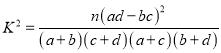 算得
算得![]() .
.
附表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过![]() 的前提下,认为“喜欢该节目与性别有关”
的前提下,认为“喜欢该节目与性别有关”
B. 在犯错误的概率不超过![]() 的前提下,认为“喜欢该节目与性别无关”
的前提下,认为“喜欢该节目与性别无关”
C. 有![]() 以上的把握认为“喜欢该节目与性别有关”
以上的把握认为“喜欢该节目与性别有关”
D. 有