题目内容
附加题:设函数f(x)=ax2+bx+c(a>b>c)满足f(1)=0,g(x)=ax+b.
设A,B是f(x)与g(x)的图象的两个交点,AA1垂直x轴于点A1,BB1垂直x轴于点B1,求线段|A1B1|长的取值范围.
【答案】分析:根据f(1)=0.得到c与a,b的关系,将f(x),g(x)两方程联立,设两根为x1,x2,则|A1B1|=|x1-x2|,通过韦达定理表示出线段|A1B1|,再根据二次函数性质求出其的取值范围.
解答:解:∵ ,
,
而a+b+c=0,⇒-c=a+b,
故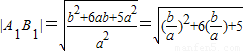 令
令 ,
,
而c=-a-b<b⇒-a<ab<2a⇒a>0,
∵a>b,
∴ ,
,
∵-a<2b,
∴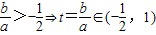 ,故
,故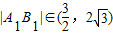 .
.
点评:本题考查了函数的变形以及二次函数的性质,是常考题型.
解答:解:∵
 ,
,而a+b+c=0,⇒-c=a+b,
故
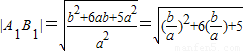 令
令 ,
,而c=-a-b<b⇒-a<ab<2a⇒a>0,
∵a>b,
∴
 ,
,∵-a<2b,
∴
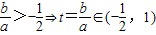 ,故
,故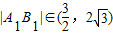 .
.点评:本题考查了函数的变形以及二次函数的性质,是常考题型.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目