题目内容
(本题满分12分)
已知{an}是一个等差数列,且a2=1,a5=-5.
(1)求数列{an}的通项an;
(2)求{an}前n项和Sn的最大值.
(1)-2n+5.(2)n=2时,Sn取到最大值4
解析试题分析:解:(1)设{an}的公差为d,
由已知条件得,
所以an=a1+(n-1)d=-2n+5.
(2)Sn=na1+d=-n2+4n=4-(n-2)2.
所以n=2时,Sn取到最大值4.
考点:数列的通项公式
点评:解决的关键是能利用等差数列的公式来结合基本量首项和公差来求解通项公式,同时能结合数列项的正负交替项来得到最值,属于基础题,或者运用二次函数性质来得到。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
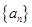 中,
中,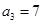 ,且
,且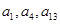 成等比数列.
成等比数列. (
(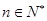 ),求数列
),求数列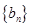 的前
的前 项和
项和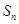 .
.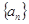 的首项为1,其前n项和为
的首项为1,其前n项和为 ,
,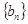 是公比为正整数的等比数列,其首项为3,前n项和为
是公比为正整数的等比数列,其首项为3,前n项和为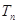 . 若
. 若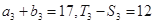 .
.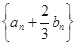 的前n项和
的前n项和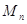 .(5分)
.(5分)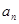 }中,
}中, ,
, ,且满足
,且满足
 ,求
,求 .
. ,1,
,1, 按某种顺序排列成等差数列.
按某种顺序排列成等差数列. 的值;
的值;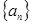 的首项、公差都为
的首项、公差都为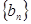 的首项、公比也都为
的首项、公比也都为 项和分别
项和分别 ,且
,且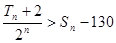 ,求满足条件的正整数
,求满足条件的正整数 是有穷等差数列,给出下面数表:
是有穷等差数列,给出下面数表:

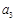 ……
…… 
 第1行
第1行
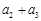 ……
…… 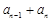 第2行
第2行 ,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为
,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为 .
. ,求和
,求和 .
. ,且
,且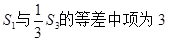
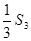 , 求和Tn=a1b1+a2b2+…+anbn
, 求和Tn=a1b1+a2b2+…+anbn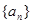 的前n项和为
的前n项和为 ,且
,且 ,(
,( =1,2,3…)
=1,2,3…)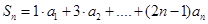 ,求
,求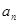 }中,
}中,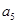 =162,公比q=3,前n项和
=162,公比q=3,前n项和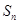 =242,求首项
=242,求首项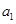 和项数n的值.
和项数n的值.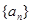 的前n项和,
的前n项和,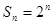 ,求
,求