题目内容
(本小题满分12分)
某甲有一个放有3个红球、2个白球、1个黄球共6个球的箱子;某乙也有一个放有3个红球、2个白球、1个黄球共6个球的箱子.
(Ⅰ)若甲在自己的箱子里任意取球,取后不放回,每次只取一个球,直到取到红球为止,求甲取球次数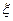 的数学期望;
的数学期望;
(Ⅱ)若甲、乙两人各从自己的箱子里任取一球比颜色,规定同色时为甲胜,异色时为乙胜,这个游戏规则公平吗?请说明理由.
某甲有一个放有3个红球、2个白球、1个黄球共6个球的箱子;某乙也有一个放有3个红球、2个白球、1个黄球共6个球的箱子.
(Ⅰ)若甲在自己的箱子里任意取球,取后不放回,每次只取一个球,直到取到红球为止,求甲取球次数
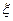 的数学期望;
的数学期望;(Ⅱ)若甲、乙两人各从自己的箱子里任取一球比颜色,规定同色时为甲胜,异色时为乙胜,这个游戏规则公平吗?请说明理由.
(Ⅰ)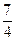 (Ⅱ)游戏规则不公平
(Ⅱ)游戏规则不公平
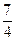 (Ⅱ)游戏规则不公平
(Ⅱ)游戏规则不公平(Ⅰ)由题意知甲取球次数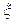 的取值为1,2,3,4
的取值为1,2,3,4
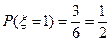 ;
;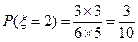 ;
;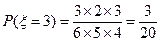 ;
;
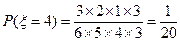
则甲取球次数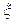 的数学期望为
的数学期望为 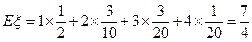
(Ⅱ)由题意,两人各自从自己箱子里任取一球比颜色共有
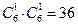 (种) 不同的情形
(种) 不同的情形
每种情形都是等可能的,记甲获胜为事件A,则
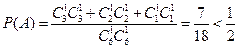
所以甲获胜的概率小于乙获胜的概率,这个游戏规则不公平。
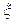 的取值为1,2,3,4
的取值为1,2,3,4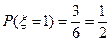 ;
;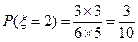 ;
;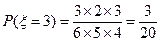 ;
;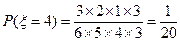
则甲取球次数
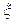 的数学期望为
的数学期望为 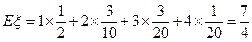
(Ⅱ)由题意,两人各自从自己箱子里任取一球比颜色共有
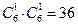 (种) 不同的情形
(种) 不同的情形每种情形都是等可能的,记甲获胜为事件A,则
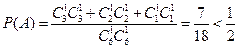
所以甲获胜的概率小于乙获胜的概率,这个游戏规则不公平。

练习册系列答案
相关题目
 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个 人的课外兴趣小组.
人的课外兴趣小组.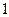 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;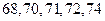 ,第二次做试验的同学得到的试验数据为
,第二次做试验的同学得到的试验数据为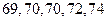 ,请问哪位同学的实验更稳定?并说明理由.
,请问哪位同学的实验更稳定?并说明理由.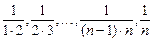 (其中n是正整数)
(其中n是正整数)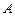 、
、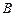 、
、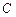 、
、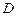 ,投掷时正面向上的概率如下表所示
,投掷时正面向上的概率如下表所示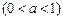 .
.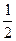
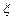 表示出现正面向上的个数.
表示出现正面向上的个数.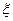 的分布列及数学期望;
的分布列及数学期望;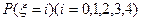 中,若
中,若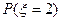 的值最大,求
的值最大,求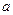 的取值范围;
的取值范围; 2)(
2)(