题目内容
已知函数f(x)= sin xcos x-cos2x-
sin xcos x-cos2x- ,x∈R.
,x∈R.
(1)求函数f(x)的最小值和最小正周期;
(2)已知△ABC内角A,B,C的对边分别为a,b,c,且c=3,f(C)=0,若向量m=(1,sin A)与n=(2,sin B)共线,求a,b的值.
【答案】
(1)f(x)min=-2,最小正周期为π;(2)a=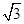 ,b=2
,b=2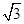 .
.
【解析】本试题主要是考查了三角函数的化简和解三角形的综合运用。
(1)利用二倍角的正弦和余弦公式化简为单一三角函数,得到周期
(2)利用第一问的结论,得到f(C)=sin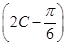 -1=0,然后利用三角方程得到角C的值。然后利用正弦定理得到b=2a,然后结合余弦定理求解得到a,b的值。
-1=0,然后利用三角方程得到角C的值。然后利用正弦定理得到b=2a,然后结合余弦定理求解得到a,b的值。
解 (1)f(x)=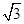 sin xcos x-cos2x-
sin xcos x-cos2x-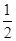 =
=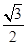 sin 2x-
sin 2x-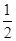 cos 2x-1=sin
cos 2x-1=sin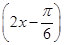 -1,
-1,
∴f(x)min=-2,最小正周期为π.
(2)∵f(C)=sin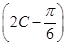 -1=0,∴sin
-1=0,∴sin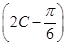 =1,∵0<C<π,-
=1,∵0<C<π,-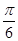 <2C-
<2C-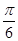 <
<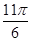 ,
,
∴2C-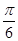 =
= ,∴C=
,∴C=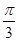 . ∵m与n共线, ∴sin
B-2sin A=0,
. ∵m与n共线, ∴sin
B-2sin A=0,
由正弦定理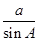 =
=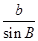 ,
得b=2a,①
,
得b=2a,①
∵c=3,由余弦定理,得9=a2+b2-2abcos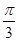 ,②
,②
由①②得:a=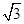 ,b=2
,b=2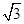 .
.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目

 x2在x=-1处取得极大值,记g(x)=
x2在x=-1处取得极大值,记g(x)= 。程序框图如图所示,若输出的结果S=
。程序框图如图所示,若输出的结果S= ,则判断框中可以填入的关于n的判断条件是( )
,则判断框中可以填入的关于n的判断条件是( )