题目内容
在△ABC中,a,b,c分别是角A,B,C的对边,且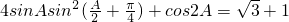
(1)求角A的大小;
(2)若角A为锐角,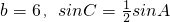 ,求c边的大小.
,求c边的大小.
解:(1)∵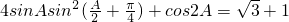
∴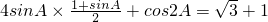
∴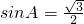
∵A∈(0,π),∴A= 或A=
或A= ;
;
(2)∵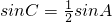 ,∴
,∴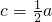
∵A= ,b=6
,b=6
∴a2=36+c2-2×6×c×cos
∴4c2=36+c2-6c
∴c2+2c-12=0
∴c=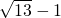
分析:(1)利用二倍角公式化简,结合A是三角形的内角,可得结论;
(2)先利用正弦定理,再利用余弦定理,解方程可得结论.
点评:本题考查二倍角公式,考查正弦、余弦定理,考查学生的计算能力,属于中档题.
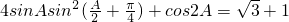
∴
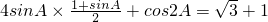
∴
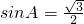
∵A∈(0,π),∴A=
 或A=
或A= ;
;(2)∵
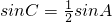 ,∴
,∴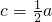
∵A=
 ,b=6
,b=6∴a2=36+c2-2×6×c×cos

∴4c2=36+c2-6c
∴c2+2c-12=0
∴c=
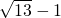
分析:(1)利用二倍角公式化简,结合A是三角形的内角,可得结论;
(2)先利用正弦定理,再利用余弦定理,解方程可得结论.
点评:本题考查二倍角公式,考查正弦、余弦定理,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.则sinA+sinB的最大值是( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|