题目内容
2.把分别标有“我”“爱”“你”的三张卡片随意的排成一排,则能使卡片从左到右可以念成“我爱你”和“你爱我”的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
分析 ,验发生包含的事件是三张卡片全排列,满足条件的事件能使卡片从左到右可以念成“我爱你”和“你爱我”,写出事件数,根据古典概型概率公式得到概率.
解答 解:由题意知本题是一个古典概型,
试验发生包含的事件是三张卡片全排列,共有A33=6种结果,
满足条件的事件是卡片排成的顺序从从左到右可以念成“我爱你”和“你爱我”,共有2种结果,
根据古典概型概率公式得到P=$\frac{2}{6}$=$\frac{1}{3}$,
故选:A.
点评 本题考查古典概型,这种问题在高考时可以作为一道解答题,古典概型要求能够列举出所有事件和发生事件的个数,本题可以列举出所有事件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知f(x)=x3-ax在(-∞,-1]上递增,则a的取值范围是( )
| A. | a>3 | B. | a≥3 | C. | a<3 | D. | a≤3 |
7.已知某海滨浴场海浪的高度y(米)是时间t (0≤t≤24,单位:小时)函数,记作:y=f(t),下表是某日各时的浪高数据:
经长期观察,y=f(t)的曲线,可以近似地看成函数y=Acos(ωt)+b的图象.
(1)根据以上数据(对浪高采用精确到0.1的数据),求出函数y=Acos(ωt)+b的最小正周期T,振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8:00时至晚上20:00时之间,有多少时间可供冲浪者进行运动?
(参考数据cos$\frac{7π}{16}$≈0.2).
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.41 | 0.88 | 0.39 | 0.91 | 1.38 | 0.90 | 0.42 | 0.89 | 1.40 |
(1)根据以上数据(对浪高采用精确到0.1的数据),求出函数y=Acos(ωt)+b的最小正周期T,振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8:00时至晚上20:00时之间,有多少时间可供冲浪者进行运动?
(参考数据cos$\frac{7π}{16}$≈0.2).
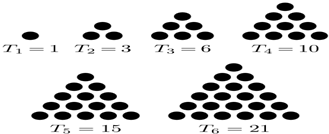 小毕喜欢把数描绘成沙滩上的小石子,他照如图所示摆成了正三角形图案,并把每个图案中总的石子个数叫做“三角形数”,记为Tn,则$\frac{1}{2{T}_{1}}$+$\frac{1}{2{T}_{2}}$+$\frac{1}{2{T}_{3}}$+…+$\frac{1}{2{T}_{2015}}$=$\frac{2015}{2016}$.
小毕喜欢把数描绘成沙滩上的小石子,他照如图所示摆成了正三角形图案,并把每个图案中总的石子个数叫做“三角形数”,记为Tn,则$\frac{1}{2{T}_{1}}$+$\frac{1}{2{T}_{2}}$+$\frac{1}{2{T}_{3}}$+…+$\frac{1}{2{T}_{2015}}$=$\frac{2015}{2016}$.