题目内容
【题目】已知定义在R上的可导函数f（x）的导函数为f'（x），满足f'（x）＜f（x），且f（x+3）为偶函数，f（6）=1，则不等式f（x）＞ex的解集为（ ）
A.（﹣∞，0）
B.（0，+∞）
C.（1，+∞）
D.（4，+∞）
【答案】A
【解析】解：设g（x）= 
，则g′（x）= 
．
∵f′（x）＜f（x），∴g′（x）＜0．∴函数g（x）是R上的减函数，
∵函数f（x+3）是偶函数，
∴函数f（﹣x+3）=f（x+3），∴函数关于x=3对称，∴f（0）=f（6）=1，
原不等式等价为g（x）＞1，∴不等式f（x）＜ex等价g（x）＞1，即g（x）＞g（0），
∵g（x）在R上单调递减，∴x＜0．
∴不等式f（x）＞ex的解集为（﹣∞，0）．
所以答案是：A．
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识，掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】学生会为了调查学生对2018年俄罗斯世界杯的关注是否与性别有关，抽样调查100人，得到如下数据：
不关注 | 关注 | 总计 | |
男生 | 30 | 15 | 45 |
女生 | 45 | 10 | 55 |
总计 | 75 | 25 | 100 |
根据表中数据，通过计算统计量K2= 
，并参考一下临界数据：
P（K2＞k0） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
若由此认为“学生对2018年俄罗斯年世界杯的关注与性别有关”，则此结论出错的概率不超过（ ）
A.0.10
B.0.05
C.0.025
D.0.01
【题目】某手机厂商推出一次智能手机，现对500名该手机使用者（200名女性，300名男性）进行调查，对手机进行打分，打分的频数分布表如下：
女性用户 | 分值区间 | [50，60） | [60，70） | [70，80） | [80，90） | [90，100） |
频数 | 20 | 40 | 80 | 50 | 10 | |
男性用户 | 分值区间 | [50，60） | [60，70） | [70，80） | [80，90） | [90，100） |
频数 | 45 | 75 | 90 | 60 | 30 |
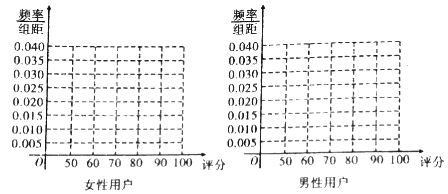
（1）完成下列频率分布直方图，并比较女性用户和男性用户评分的方差大小（不计算具体值，给出结论即可）；
（2）根据评分的不同，运用分层抽样从男性用户中抽取20名用户，在这20名用户中，从评分不低于80分的用户中任意取3名用户，求3名用户评分小于90分的人数的分布列和期望．
