题目内容
如图,在直三棱柱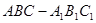 中,
中,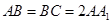
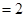 ,
,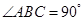 ,
,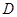 是
是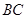 的中点.
的中点.
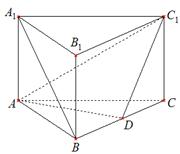
(1)求证: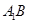 平行平面
平行平面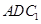 ;
;
(2)求二面角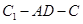 的余弦值;
的余弦值;
(3)试问线段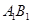 上是否存在点
上是否存在点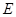 ,使
,使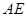 与
与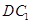 成
成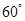 角?若存在,确定
角?若存在,确定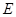 点位置,若不存在,说明理由.
点位置,若不存在,说明理由.
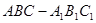 中,
中,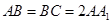
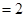 ,
,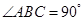 ,
,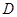 是
是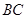 的中点.
的中点.
(1)求证:
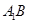 平行平面
平行平面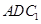 ;
;(2)求二面角
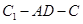 的余弦值;
的余弦值;(3)试问线段
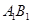 上是否存在点
上是否存在点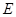 ,使
,使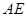 与
与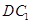 成
成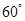 角?若存在,确定
角?若存在,确定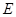 点位置,若不存在,说明理由.
点位置,若不存在,说明理由.(1)只需证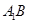 ∥
∥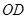 ;(2)
;(2)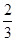 ;(3)点
;(3)点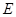 为线段
为线段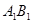 中点时,
中点时,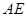 与
与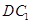 成
成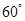 角.
角.
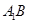 ∥
∥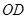 ;(2)
;(2)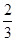 ;(3)点
;(3)点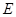 为线段
为线段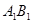 中点时,
中点时,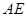 与
与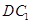 成
成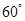 角.
角.试题分析:(Ⅰ)证明:连结
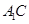 ,交
,交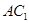 于点
于点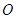 ,连结
,连结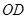 .
.由
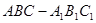 是直三棱柱,
是直三棱柱,得 四边形
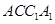 为矩形,
为矩形,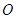 为
为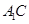 的中点.
的中点.又
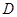 为
为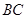 中点,所以
中点,所以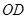 为
为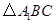 中位线,
中位线,所以
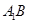 ∥
∥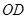 ,
, 因为
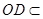 平面
平面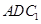 ,
,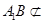 平面
平面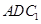 ,
, 所以
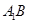 ∥平面
∥平面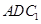 .
. (Ⅱ)由
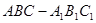 是直三棱柱,且
是直三棱柱,且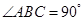 ,故
,故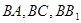 两两垂直.
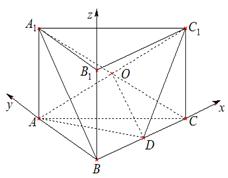
两两垂直.如图建立空间直角坐标系
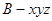 .设
.设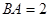 ,
,
则
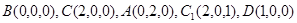 .
.所以
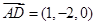 ,
,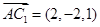
设平面
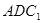 的法向量为
的法向量为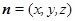 ,则有
,则有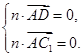
所以
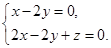 取
取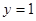 ,得
,得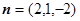 .
.易知平面
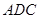 的法向量为
的法向量为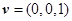 .
. 由二面角
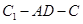 是锐角,得
是锐角,得 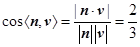 .
. 所以二面角
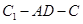 的余弦值为
的余弦值为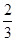 .
.(Ⅲ)假设存在满足条件的点
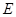 .
.因为
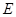 在线段
在线段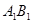 上,
上,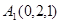 ,
,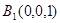 ,故可设
,故可设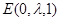 ,其中
,其中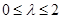 .
.所以
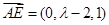 ,
,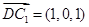 .
. 因为
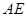 与
与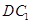 成
成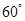 角,所以
角,所以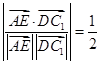 .
. 即
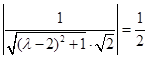 ,解得
,解得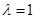 ,舍去
,舍去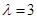 .
. 所以当点
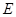 为线段
为线段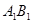 中点时,
中点时,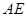 与
与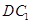 成
成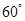 角.
角. 点评:二面角的求法是立体几何中的一个难点。我们解决此类问题常用的方法有两种:①综合法,综合法的一般步骤是:一作二说三求。②向量法,运用向量法求二面角应注意的是计算。很多同学都会应用向量法求二面角,但结果往往求不对,出现的问题就是计算错误。

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
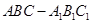 中,
中,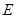 、
、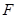 分别是
分别是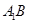 、
、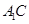 的中点,点
的中点,点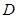 在
在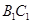 上,
上,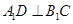 。
。
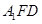
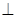 平面
平面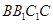
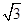 ,VA =" 6."
,VA =" 6." 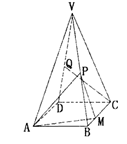
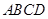 -
-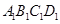 中,
中,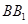 与平面
与平面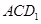 所成角的余弦值为 .
所成角的余弦值为 .  、
、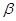 表示不同平面,下列命题正确的是 ( )
表示不同平面,下列命题正确的是 ( )
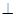

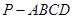 中,侧棱
中,侧棱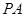 的长为
的长为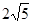 ,
,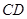 所成的角的大小等于
所成的角的大小等于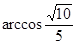 .
.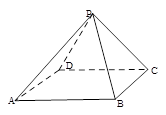
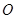 的表面上,求此球
的表面上,求此球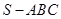 中,
中,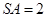 ,
,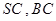 的中点分别为
的中点分别为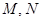 ,且
,且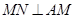 ,则正三棱锥
,则正三棱锥