题目内容
正方体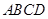 -
-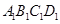 中,
中,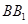 与平面
与平面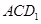 所成角的余弦值为 .
所成角的余弦值为 .
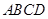 -
-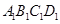 中,
中,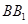 与平面
与平面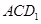 所成角的余弦值为 .
所成角的余弦值为 . 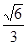
试题分析:设上下底面的中心分别为O1,O,则O1O与平面ACD1所成角就是BB1与平面ACD1所成角,cos∠O1OD1=
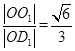 。
。点评:本小题主要考查正方体的性质、直线与平面所成的角、点到平面的距离的求法,利用等体积转化求出D到平面ACD1的距离是解决本题的关键所在,这也是转化思想的具体体现.注:线面角的范围为:
 。
。
练习册系列答案
相关题目
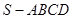 的底面边长为2,高为2,
的底面边长为2,高为2,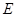 为边
为边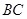 的中点,动点
的中点,动点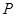 在表面上运动,并且总保持
在表面上运动,并且总保持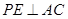 ,则动点
,则动点
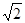
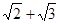
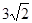
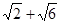
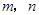 是两条不同的直线,
是两条不同的直线,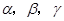 是三个不同的平面,则下列命题中的真命题是( )
是三个不同的平面,则下列命题中的真命题是( ) ,则
,则

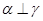 ,
, ,则
,则
 ,
,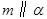 ,则
,则
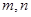 ,两个不同的平面
,两个不同的平面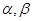 ,则下列命题中正确的是( )
,则下列命题中正确的是( ) 则
则
 则
则
 则
则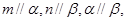 则
则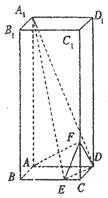
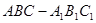 中,
中,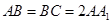
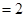 ,
,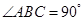 ,
,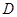 是
是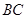 的中点.
的中点.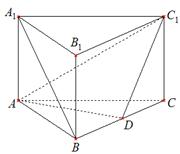
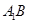 平行平面
平行平面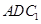 ;
;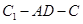 的余弦值;
的余弦值;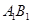 上是否存在点
上是否存在点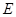 ,使
,使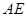 与
与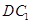 成
成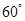 角?若存在,确定
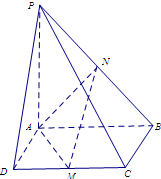
角?若存在,确定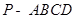 ,底面
,底面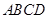 是正方形,
是正方形,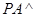 面
面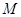 是
是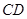 的中点,点
的中点,点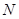 是
是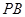 的中点,连接
的中点,连接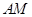 ,
,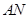
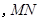 .
.
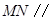 面
面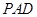 ;
;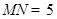 ,
,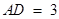 ,求二面角
,求二面角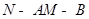 的余弦值.
的余弦值. 中,
中, ,
,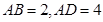 将
将 沿
沿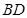 折起到
折起到 的位置,使平面
的位置,使平面 平面
平面

 ;
;  的侧面积.
的侧面积.