题目内容
若直线y=x+m与曲线y2=x有两个不同的交点,则实数m的取值范围为分析:把y=x+m 代入曲线y2=x化简可得y2-y+m=0 有两个不同的实数解,由判别式大于解得实数m的取值范围.
解答:解:把y=x+m 代入曲线y2=x化简可得y2-y+m=0 有两个不同的实数解,
故判别式△=1-4m>0,∴m<
,
故答案为 (-∞,
).
故判别式△=1-4m>0,∴m<
| 1 |
| 4 |
故答案为 (-∞,
| 1 |
| 4 |
点评:本题考查一元二次方程有两个实数解的条件,由条件得到y2-y+m=0 有两个不同的实数解,是解题的关键.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
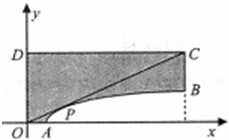 已知图形OAPBCD是由不等式组
已知图形OAPBCD是由不等式组