题目内容
.将编号为1,2,3的三个小球随意放入编号为1,2,3的三个纸箱中,每个纸箱内有且只有一个小球,称此为一轮“放球”,设一轮“放球”后编号为i(i=1,2,3)的纸箱放入的小球编号为ai,定义吻合度误差为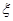 =|1-a1|+|2-a2|+|3-a3|。假设a1,a2,a3等可能地为1、2、3的各种排列,求⑴某人一轮“放球”满足
=|1-a1|+|2-a2|+|3-a3|。假设a1,a2,a3等可能地为1、2、3的各种排列,求⑴某人一轮“放球”满足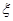 =2时的概率。⑵
=2时的概率。⑵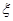 的数学期望。
的数学期望。
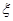 =|1-a1|+|2-a2|+|3-a3|。假设a1,a2,a3等可能地为1、2、3的各种排列,求⑴某人一轮“放球”满足
=|1-a1|+|2-a2|+|3-a3|。假设a1,a2,a3等可能地为1、2、3的各种排列,求⑴某人一轮“放球”满足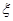 =2时的概率。⑵
=2时的概率。⑵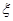 的数学期望。
的数学期望。解:⑴
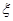 的所有可能结果如下:
的所有可能结果如下:
|
| ||||||||||||||||||||||||||||
| ∴P( 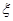 ="2)=" ="2)=" 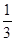 …………(6分) …………(6分) |
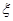 的分布列为
的分布列为
| ∴ 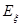 =2× =2×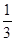 +4× +4×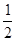 = =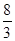  …(6分) …(6分) |
略

练习册系列答案
相关题目
 是离散型随机变量,
是离散型随机变量,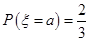 ,
,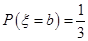 ,且a<b,又Eξ=
,且a<b,又Eξ=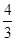 ,Dξ=
,Dξ=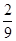 ,则a+b的值为( )
,则a+b的值为( )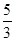


 0.785,汽车的碳排放量(千克)=油耗公升数
0.785,汽车的碳排放量(千克)=油耗公升数
 表示25个人中低碳族人数,求E
表示25个人中低碳族人数,求E 用户推出了多款
用户推出了多款 ;选择
;选择 ;选择
;选择 ;他们的选择相互独立.设在该时段这三名学生中选择
;他们的选择相互独立.设在该时段这三名学生中选择 ,求随机变量
,求随机变量 .
. 现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用
现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用 表示取球终止所需要的取球次数.
表示取球终止所需要的取球次数.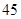 名,女同学有
名,女同学有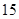 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个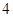 人的课外兴趣小组.
人的课外兴趣小组.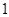 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率; ξ∈N)~正态
ξ∈N)~正态 .3,估计该班学
.3,估计该班学