题目内容
【题目】已知函数f（x）=lg（x2+tx+2）（t为常数，且﹣2 
＜t＜2 ）．
（1）当x∈[0，2]时，求函数f（x）的最小值（用t表示）；
（2）是否存在不同的实数a，b，使得f（a）=lga，f（b）=lgb，并且a，b∈（0，2）．若存在，求出实数t的取值范围；若不存在，请说明理由．
【答案】
（1）解：令g（x）=x2+tx+2对称轴为x=﹣ 
，
② 当﹣ ≤0，即t≥0时，g（x）min=g（0）=2，∴f（x）min=lg2；
②当0＜﹣ ＜2，即﹣4＜t＜0时，g（x）min=g（﹣ ）=2﹣ 
，
考虑到g（x）＞0，则
1°﹣2 
＜t＜0，f（x）min=f（﹣ ）=lg（2﹣ ），
2°﹣4＜t≤﹣2 ，没有最小值．
③当﹣ ≥2，即t≤﹣4时，g（x）min=g（2）=6+2t，
考虑到g（x）＞0∴f（x）没有最小值．
综上所述：当t≤﹣2时f（x）没有最小值；
当t＞﹣2时，f（x）min=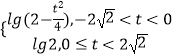 
（2）解：假设存在，则由已知等价于x2+tx+2=x在区间（0，2）上有两个不同的实根，
等价于t=﹣（ 
+x）+1，x∈（0，2）
t′=﹣1+ 
，x∈（0， ），t′＞0；x∈（ ，2），t′＜0．
x= 取最大值1﹣2 ．x=2，t=﹣2．
可得﹣2＜t＜1﹣2 ．
故存在，实数t的取值范围是﹣2＜t＜1﹣2
【解析】（1）令g（x）=x2+tx+2，要求函数f（x）的最小值，根据复合函数的单调性可知，只要求解函数g（x）的最小值即可，结合图象，需判断对称轴与区间[0，2]的位置关系，分类讨论；（2）假设存在，则由已知等价于x2+tx+2=x在区间（0，2）上有两个不同的实根，分离参数，运用导数求出右边的最值和范围，即可得出结论．
【考点精析】关于本题考查的函数的最值及其几何意义和二次函数在闭区间上的最值，需要了解利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值；当
时，当
时，
；当
时在
上递减，当时，
才能得出正确答案．
