题目内容
如果两个相交平面都垂直于第三个平面，那么它们的交线也垂直于这个平面。
已知：β⊥α，γ⊥α，β
γ=a
求证：a⊥α
已知：β⊥α，γ⊥α，β
γ=a求证：a⊥α利用线面垂直的性质定理
证明：设αβ=AB，αγ=CD
在平面β内作L1⊥AB，
在平面γ内作L1⊥CD，
∵α⊥β∴L1⊥α
同理L2⊥α
∴L1//L2
∴L1//β
∴L1//a
∴a⊥α
证明：设α
β=AB，αγ=CD在平面β内作L1⊥AB，
在平面γ内作L1⊥CD，
∵α⊥β∴L1⊥α
同理L2⊥α
∴L1//L2
∴L1//β
∴L1//a
∴a⊥α
练习册系列答案
相关题目
在平面
内，过点
和
，应该怎样画线？
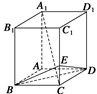
CC1.
