题目内容
(12分) 已知函数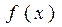 是偶函数,且在(0,+∞)上的减函数,判断f(x)在(-∞,0)上是增函数还是减函数,并证明你的结论。
是偶函数,且在(0,+∞)上的减函数,判断f(x)在(-∞,0)上是增函数还是减函数,并证明你的结论。
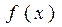 是偶函数,且在(0,+∞)上的减函数,判断f(x)在(-∞,0)上是增函数还是减函数,并证明你的结论。
是偶函数,且在(0,+∞)上的减函数,判断f(x)在(-∞,0)上是增函数还是减函数,并证明你的结论。略
解:f(x)在(-∞,0)上为增函数
设x1,x2∈(-∞,0),且x1<x2,则-x1>-x2>0
而f(x)是偶函数且在(0,+∞)是减函数
∴f(-x1)>f(-x2)
∴f(x1) - f(x2) =" f(-x1)" - f(-x2) <0
即f(x1) < f(x2) ,所以f(x)在(-∞,0)上为增函数
设x1,x2∈(-∞,0),且x1<x2,则-x1>-x2>0
而f(x)是偶函数且在(0,+∞)是减函数
∴f(-x1)>f(-x2)
∴f(x1) - f(x2) =" f(-x1)" - f(-x2) <0
即f(x1) < f(x2) ,所以f(x)在(-∞,0)上为增函数

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
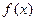 的定义域为
的定义域为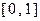 ,且同时满足:①
,且同时满足:①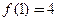 ;②若
;②若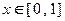 ,都有
,都有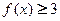 ;③若
;③若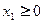 ,
,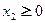 ,
,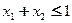 ,都有
,都有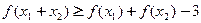 .
.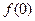 的值;
的值;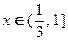 时,求证:
时,求证: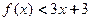 .
.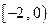 ∪
∪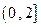 上的奇函数,当
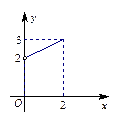
上的奇函数,当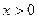 时,f (x)的图象如右图所示,那么f (x)的值域是
时,f (x)的图象如右图所示,那么f (x)的值域是 

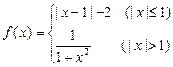 ,则
,则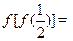 ( )
( )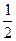
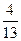
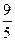
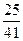
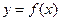 满足:①
满足:①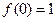 ;②
;②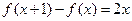 。
。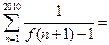 _____.
_____. 在
在 上的减函数,则
上的减函数,则 的取值范围是
的取值范围是



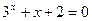 和方程
和方程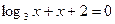 的根分别为
的根分别为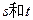 ,若函数
,若函数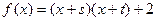 ,则 ( )
,则 ( )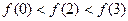 B
B 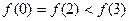
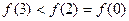 D
D 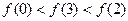
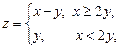 若-2≤x≤2,-2≤y≤2,则z的最小值为
若-2≤x≤2,-2≤y≤2,则z的最小值为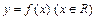 满足:对一切
满足:对一切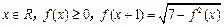 ;当
;当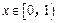 时,
时,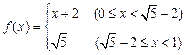 , 则
, 则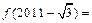 ( )
( )