题目内容
已知直线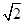 ax+by=1(a,b是实数)与圆O:x2+y2=1(O是坐标原点)相交于A,B两点,且△AOB是直角三角形,点P(a,b)是以点M(0,1)为圆心的圆M上的任意一点,则圆M的面积的最小值为________.
ax+by=1(a,b是实数)与圆O:x2+y2=1(O是坐标原点)相交于A,B两点,且△AOB是直角三角形,点P(a,b)是以点M(0,1)为圆心的圆M上的任意一点,则圆M的面积的最小值为________.
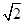 ax+by=1(a,b是实数)与圆O:x2+y2=1(O是坐标原点)相交于A,B两点,且△AOB是直角三角形,点P(a,b)是以点M(0,1)为圆心的圆M上的任意一点,则圆M的面积的最小值为________.
ax+by=1(a,b是实数)与圆O:x2+y2=1(O是坐标原点)相交于A,B两点,且△AOB是直角三角形,点P(a,b)是以点M(0,1)为圆心的圆M上的任意一点,则圆M的面积的最小值为________.(3-2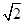 )π
)π
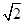 )π
)π因为直线与圆O相交所得△AOB是直角三角形,可知∠AOB=90°,所以圆心O到直线的距离为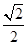 =
=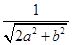 ,所以a2=1-
,所以a2=1-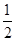 b2≥0,即-
b2≥0,即-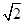 ≤b≤
≤b≤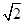 .设圆M的半径为r,则r=|PM|=
.设圆M的半径为r,则r=|PM|=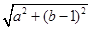 =
=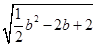 =
=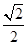 (2-b),又-
(2-b),又-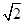 ≤b≤
≤b≤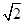 ,所以
,所以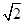 +1≥|PM|≥
+1≥|PM|≥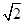 -1,所以圆M的面积的最小值为(3-2
-1,所以圆M的面积的最小值为(3-2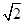 )π.
)π.
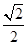 =
=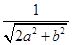 ,所以a2=1-
,所以a2=1-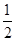 b2≥0,即-
b2≥0,即-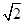 ≤b≤
≤b≤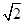 .设圆M的半径为r,则r=|PM|=
.设圆M的半径为r,则r=|PM|=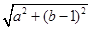 =
=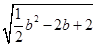 =
=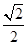 (2-b),又-
(2-b),又-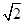 ≤b≤
≤b≤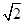 ,所以
,所以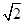 +1≥|PM|≥
+1≥|PM|≥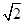 -1,所以圆M的面积的最小值为(3-2
-1,所以圆M的面积的最小值为(3-2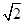 )π.
)π.
练习册系列答案
相关题目
 的三个顶点
的三个顶点 ,
,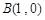 ,
,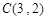 ,其外接圆为
,其外接圆为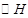 .
.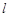 过点
过点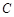 ,且被
,且被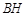 上的任意一点
上的任意一点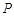 ,若在以
,若在以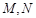 ,使得点
,使得点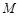 是线段
是线段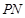 的中点,求
的中点,求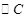 的半径
的半径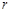 的取值范围.
的取值范围.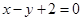 与圆C:
与圆C: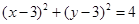 相交于A、B两点,则
相交于A、B两点,则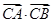 的值为( )
的值为( )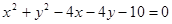 上至少有三个不同的点到直线
上至少有三个不同的点到直线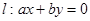 的距离为
的距离为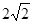 ,则直线
,则直线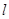 的倾斜角的取值范围是( )
的倾斜角的取值范围是( )

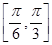

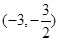 且被圆x2+y2=25截得的弦长是8,则该直线的方程为( ).
且被圆x2+y2=25截得的弦长是8,则该直线的方程为( ).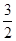
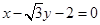 将圆
将圆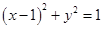 分割成的两段圆孤长之比为( )
分割成的两段圆孤长之比为( )



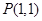 的直线将圆形区域
的直线将圆形区域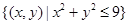 分成两部分,使得两部分的面积相差最大,则该直线的方程是( )
分成两部分,使得两部分的面积相差最大,则该直线的方程是( )

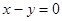

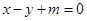 与圆
与圆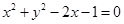 有两个不同交点的一个充分不必要条件是( )
有两个不同交点的一个充分不必要条件是( )


