题目内容
若直线过点P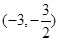 且被圆x2+y2=25截得的弦长是8,则该直线的方程为( ).
且被圆x2+y2=25截得的弦长是8,则该直线的方程为( ).
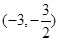 且被圆x2+y2=25截得的弦长是8,则该直线的方程为( ).
且被圆x2+y2=25截得的弦长是8,则该直线的方程为( ).| A.3x+4y+15=0 | B.x=-3或y=-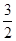 |
| C.x=-3 | D.x=-3或3x+4y+15=0 |
D
若直线的斜率不存在,则该直线的方程为x=-3,代入圆的方程解得y=±4,故该直线被圆截得的弦长为8,满足条件;若直线的斜率存在,不妨设直线的方程为y+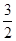 =k(x+3),即kx-y+3k-
=k(x+3),即kx-y+3k-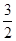 =0,因为该直线被圆截得的弦长为8,故半弦长为4,又圆的半径为5,则圆心(0,0)到直线的距离为
=0,因为该直线被圆截得的弦长为8,故半弦长为4,又圆的半径为5,则圆心(0,0)到直线的距离为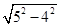 =
=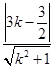 ,解得k=-
,解得k=-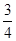 ,此时该直线的方程为3x+4y+15=0.
,此时该直线的方程为3x+4y+15=0.
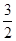 =k(x+3),即kx-y+3k-
=k(x+3),即kx-y+3k-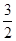 =0,因为该直线被圆截得的弦长为8,故半弦长为4,又圆的半径为5,则圆心(0,0)到直线的距离为
=0,因为该直线被圆截得的弦长为8,故半弦长为4,又圆的半径为5,则圆心(0,0)到直线的距离为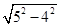 =
=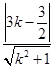 ,解得k=-
,解得k=-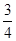 ,此时该直线的方程为3x+4y+15=0.
,此时该直线的方程为3x+4y+15=0.
练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
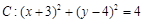 .
. 过点
过点 ,且与圆
,且与圆 相切,求直线
相切,求直线 的半径为4,圆心
的半径为4,圆心 :
: 上,且与圆
上,且与圆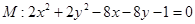 ,直线
,直线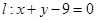 ,过
,过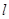 上一点A作
上一点A作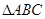 ,使得
,使得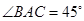 ,边AB过圆心M,且B,C在圆M上,求点A纵坐标的取值范围。
,边AB过圆心M,且B,C在圆M上,求点A纵坐标的取值范围。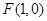 ,并且与直线
,并且与直线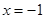 相切,若动圆C与直线
相切,若动圆C与直线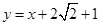 总有公共点,则圆C的面积( )
总有公共点,则圆C的面积( )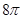
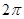

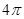
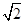
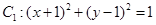 ,圆
,圆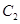 与圆
与圆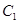 关于直线
关于直线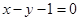 对称,则圆
对称,则圆
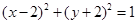


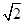 ax+by=1(a,b是实数)与圆O:x2+y2=1(O是坐标原点)相交于A,B两点,且△AOB是直角三角形,点P(a,b)是以点M(0,1)为圆心的圆M上的任意一点,则圆M的面积的最小值为________.
ax+by=1(a,b是实数)与圆O:x2+y2=1(O是坐标原点)相交于A,B两点,且△AOB是直角三角形,点P(a,b)是以点M(0,1)为圆心的圆M上的任意一点,则圆M的面积的最小值为________. 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为 ,
, ,则直线
,则直线 的方程为( )
的方程为( )