题目内容
在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=![]() .
.
(Ⅰ)求四棱锥S-ABCD的体积;
(Ⅱ)求面SCD与面SBA所成的二面角的正切值.
解:(Ⅰ)直角梯形ABCD的面积是:![]()
∴四棱锥S-ABCD的体积是:![]()
(Ⅱ)延长BA、CD相交于点E,连结SE,则SE是所求二面角的棱;
∵AD∥BC,BC=2AD ∴EA=AB=SA,∴SE⊥S(B)
∵SA⊥面ABCD,得面SEB⊥面EBC,EB是交线,又BC⊥EB,
∴BC⊥平面SEB,故SB是SC在面SEB上的射影,
∴CS⊥SE,故∠BSC是所求二面角的平面角.
∵![]() ,BC=1,BC⊥SB
,BC=1,BC⊥SB
∴![]()
即所求二面角的正切值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
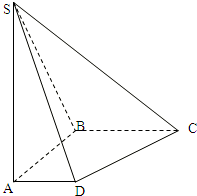 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=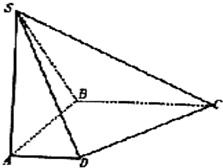 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,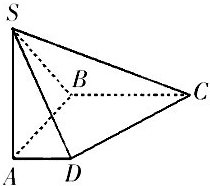 如图在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,
如图在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD, 如图,在底面是直角梯形的四棱锥S-ABCD中,已知∠ABC=90°,SA⊥平面ABCD,AB=BC=2,AD=1.
如图,在底面是直角梯形的四棱锥S-ABCD中,已知∠ABC=90°,SA⊥平面ABCD,AB=BC=2,AD=1. (2010•宝山区模拟)在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=
(2010•宝山区模拟)在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=