题目内容
已知抛物线C的方程为y2=2x，焦点为F，过抛物线C的准线与x轴的交点的直线为l。
（1）若直线l与抛物线C交于A、B两点，且|FA|=2|FB|，求k的值；
（2）设点P是抛物线C上的动点，点R、N在y轴上，圆（x- 1）2+y2=1内切于△PRN，求△PRN面积的最小值。
（1）若直线l与抛物线C交于A、B两点，且|FA|=2|FB|，求k的值；
（2）设点P是抛物线C上的动点，点R、N在y轴上，圆（x- 1）2+y2=1内切于△PRN，求△PRN面积的最小值。
解：（1）由题意可知，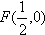
，准线为
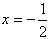
设直线l为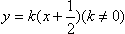
A（x1，y1），B（x2，y2）
由|FA|=2|FB|，得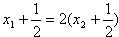
即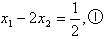
由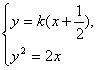
得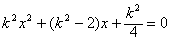
故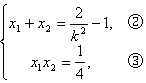
解由①②③构成的方程组得x1=1，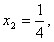
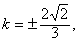
又由Δ=（k2-2）2-k4=4-4k2>0，得-1＜k＜1且k≠0，
故所求得的k值适合，
因此所求的k值为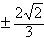
。
（2）设P（x0，y0），R（0，b），N（0，c），且b>c，
∴直线PR的方程为（y0-b）x-x0y+x0b=0
∵圆（x-1）2+y2=1内切于△PRN，
∴圆心（1，0）到直线PR的距离为1，
即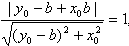
化简得（x0-2）b2+ 2y0b-x0=0，
同理可得（x0-2）c2+2y0c-x0=0，
由题意可知x0>2，
所以b、c为方程（x0-2）x2+2y0x-x0=0的两根
∴
∴
∴
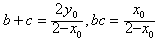
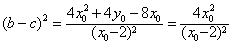
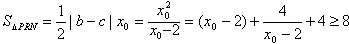
当且仅当x0=4时取等号，
所以△PRN面积的最小值为8。
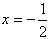
，准线为设直线l为
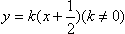
A（x1，y1），B（x2，y2）
由|FA|=2|FB|，得
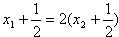
即
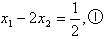
由
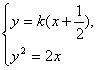
得
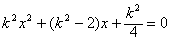
故
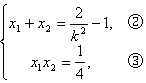
解由①②③构成的方程组得x1=1，
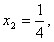
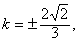
又由Δ=（k2-2）2-k4=4-4k2>0，得-1＜k＜1且k≠0，
故所求得的k值适合，
因此所求的k值为
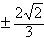。（2）设P（x0，y0），R（0，b），N（0，c），且b>c，
∴直线PR的方程为（y0-b）x-x0y+x0b=0
∵圆（x-1）2+y2=1内切于△PRN，
∴圆心（1，0）到直线PR的距离为1，
即
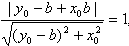
化简得（x0-2）b2+ 2y0b-x0=0，
同理可得（x0-2）c2+2y0c-x0=0，
由题意可知x0>2，
所以b、c为方程（x0-2）x2+2y0x-x0=0的两根
∴
∴
∴
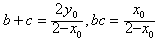
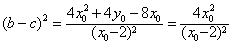
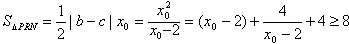
当且仅当x0=4时取等号，
所以△PRN面积的最小值为8。
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
（2011•合肥三模）已知抛物线C的方程为x2=2py（p＞0），过抛物线上点M（-2
已知抛物线C的方程为x2=2py（p＞0），焦点F为 （0，1），点P（x1，y1）是抛物线上的任意一点，过点P作抛物线的切线交抛物线的准线l于点A（s，t）．