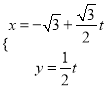题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,椭圆上一点
,椭圆上一点![]() 与椭圆右焦点的连线垂直于
与椭圆右焦点的连线垂直于![]() 轴.
轴.
(1)求椭圆![]() 的方程;
的方程;
(2)与抛物线![]() 相切于第一象限的直线
相切于第一象限的直线![]() ,与椭圆
,与椭圆![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求直线
,求直线![]() 斜率的最小值.
斜率的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)因为![]() 轴,所以
轴,所以![]()
![]() 点代入方程得:
点代入方程得:![]() ,又
,又![]() ,可得方程
,可得方程![]() ;(2)设切点为
;(2)设切点为 ,因为
,因为![]() ,对
,对![]() 求导,
求导,![]() ,所以切线斜率为
,所以切线斜率为![]() ,所以切线方程为:
,所以切线方程为:![]() ,与椭圆联立,写出韦达定理,可求出
,与椭圆联立,写出韦达定理,可求出![]() 的中点坐标
的中点坐标![]() ,进而写出中垂线的方程,得到
,进而写出中垂线的方程,得到![]() 点坐标,根据
点坐标,根据![]() 的坐标写出
的坐标写出![]() 用
用![]() 表示,利用基本不等式放缩即可求得最小值,注意验证取等条件.
表示,利用基本不等式放缩即可求得最小值,注意验证取等条件.
试题解析:解:(1)![]() 点
点![]() 与椭圆右焦点的连线垂直于
与椭圆右焦点的连线垂直于![]() 轴,
轴,
![]() ,将
,将![]() 点坐标代入椭圆方程可得
点坐标代入椭圆方程可得![]() .
.
又![]() ,联立可解得
,联立可解得![]() ,
,![]() ,
,
所以椭圆的方程为![]() .
.
(2)设切点坐标为,![]() ,则
,则![]() .
.
整理,得![]() ,
,
![]() .
.
设![]() ,
,![]() ,
,
联立直线方程和椭圆方程可得![]() ,
,

![]() 的中点坐标为
的中点坐标为 ,
,
![]() 的垂直平分线方程为
的垂直平分线方程为 ,令
,令![]() ,得
,得 .
.
即 ,
,![]() .
.
![]() ,
, ,
,
当且仅当![]() 时取得等号.
时取得等号.
![]() 直线
直线![]() 的斜率的最小值为
的斜率的最小值为![]() .
.

 特高级教师点拨系列答案
特高级教师点拨系列答案【题目】某房屋开发公司根据市场调查,计划在2017年开发的楼盘中设计“特大套”、“大套”、“经济适
用房”三类商品房,每类房型中均有舒适和标准两种型号.某年产量如下表:
房型 | 特大套 | 大套 | 经济适用房 |
舒适 | 100 | 150 |
|
标准 | 300 |
| 600 |
若按分层抽样的方法在这一年生产的套房中抽取50套进行检测,则必须抽取“特大套”套房10套, “大套”15套.
(1)求![]() ,
,![]() 的值;
的值;
(2)在年终促销活动中,奖给了某优秀销售公司2套舒适型和3套标准型“经济适用型”套房,该销售公司又从中随机抽取了2套作为奖品回馈消费者.求至少有一套是舒适型套房的概率;
(3)今从“大套”类套房中抽取6套,进行各项指标综合评价,并打分如下:
![]()
现从上面6个分值中随机的一个一个地不放回抽取,规定抽到数9.6或9.7,抽取工作即停止.记在抽取到数9.6或9.7所进行抽取的次数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.