题目内容
已知函数 ,
,
(1)讨论函数 的单调性;
的单调性;
(2)证明:若 ,则对于任意
,则对于任意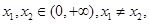 有
有 。
。
(1)a=2时, 在
在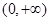 上单调增加;
上单调增加;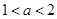 时,
时, 在
在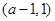 上单调减少,在
上单调减少,在 ,
,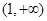 上单调增加;
上单调增加;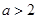 时,
时, 在(1,a-1)上单调减少,在(0,1),(a-1,+?)上单调增加;
在(1,a-1)上单调减少,在(0,1),(a-1,+?)上单调增加;
(2)证明详见解析
解析试题分析:(1)求导,利用导数分类求单调性;(2)先求导,然后求出单间区间,在进一步证明即可.
试题解析:(1) 的定义域为
的定义域为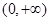 ,
,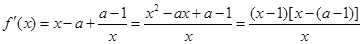
(i)若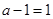 ,即a=2,则
,即a=2,则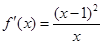 ,故
,故 在
在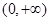 上单调增加。
上单调增加。
(ii)若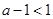 ,而
,而 ,故
,故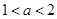 ,则当
,则当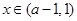 时,
时,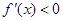 ;
;
当 及
及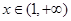 时,
时,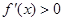 。
。
故 在
在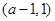 上单调减少,在
上单调减少,在 ,
,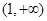 上单调增加。
上单调增加。
(iii)若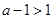 ,即
,即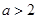 , 同理可得
, 同理可得 在(1,a-1)上单调减少,在(0,1),(a-1,+?)上单调增加。
在(1,a-1)上单调减少,在(0,1),(a-1,+?)上单调增加。
(2)考虑函数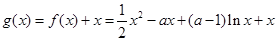 ,
,
则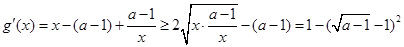 ,
,
由于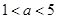 ,故
,故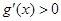 ,即
,即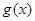 在
在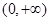 上单调增加,从而当
上单调增加,从而当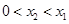 时,
时,
有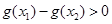 ,即
,即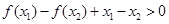 ,故
,故 ;
;
当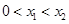 时,有
时,有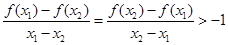 。
。
考点:1.求函数的导数;2.利用导数求函数的单调性.

练习册系列答案
相关题目
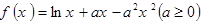 .
.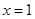 是函数
是函数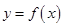 的极值点,求
的极值点,求 的值;
的值;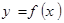 的单调区间.
的单调区间.
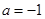 ,
,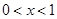 时,
时,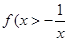 ;
; 在定义域内的零点个数,并证明你的结论.
在定义域内的零点个数,并证明你的结论. 在
在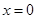 处取得极值,且曲线
处取得极值,且曲线 在点
在点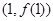 处的切线垂直于直线
处的切线垂直于直线 .
.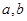 的值;
的值; ,讨论
,讨论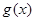 的单调性.
的单调性.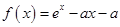 .
.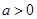 ,
,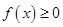 对一切
对一切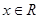 恒成立,求
恒成立,求 的最大值;
的最大值;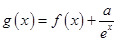 ,且
,且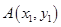 、
、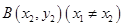 是曲线
是曲线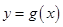 上任意两点,若对任意
上任意两点,若对任意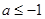 ,直线
,直线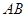 的斜率恒大于常数
的斜率恒大于常数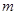 ,求
,求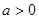 ,函数
,函数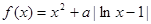
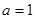 时,求曲线
时,求曲线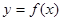 在
在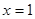 处的切线方程;
处的切线方程;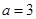 时,求函数
时,求函数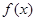 的单调区间;
的单调区间;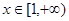 时,求函数
时,求函数 -lnx,x∈[1,3].
-lnx,x∈[1,3].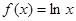 ,若
,若
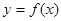 在点
在点 处的切线方程;
处的切线方程; 在区间
在区间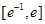 上有两个零点,求实数b的取值范围;
上有两个零点,求实数b的取值范围;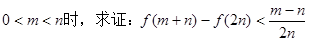
 ,函数
,函数
 在点
在点 处的切线方程; (2)当
处的切线方程; (2)当 时,求
时,求 的最大值.
的最大值.