题目内容
(本小题满分12分)
已知各项均为正数的数列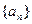 满足:
满足:
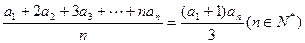
(I)求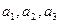 的值,猜测
的值,猜测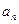 的表达式并给予证明;
的表达式并给予证明;
(II)求证: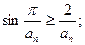
(III)设数列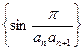 的前n项和为
的前n项和为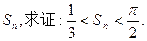
已知各项均为正数的数列
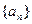 满足:
满足: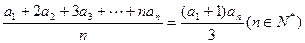
(I)求
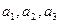 的值,猜测
的值,猜测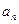 的表达式并给予证明;
的表达式并给予证明;(II)求证:
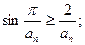
(III)设数列
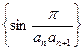 的前n项和为
的前n项和为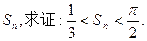
略
解:(Ⅰ)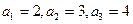 ,
,
猜测: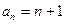
下用数学归纳法
①当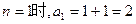 ,猜想
,猜想 成立;
成立;
②假设当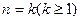 时猜想成立,即
时猜想成立,即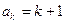
由条件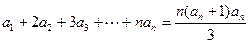
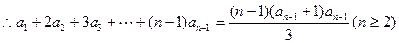
两式相减得:
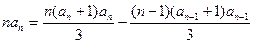
则当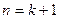 时,
时,
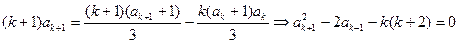
 时,猜想也成立
时,猜想也成立
故对一切的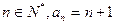 成立
成立
(Ⅱ)设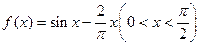
由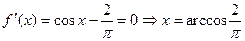
由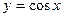 的单调
的单调 性知
性知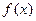 在
在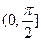 内有且只有一个极大值点,
内有且只有一个极大值点,
且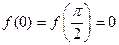
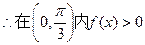
即
令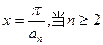 时有
时有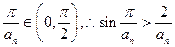
又当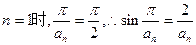
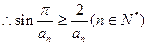
(Ⅲ)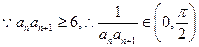
由(Ⅱ)可知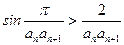
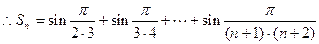
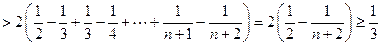
即对一切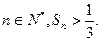
又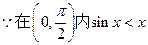
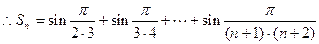
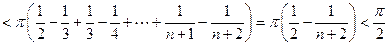
即对一切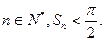
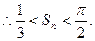
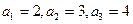 ,
,猜测:
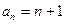
下用数学归纳法
①当
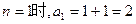 ,猜想
,猜想 成立;
成立;②假设当
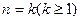 时猜想成立,即
时猜想成立,即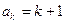
由条件
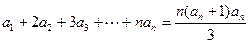
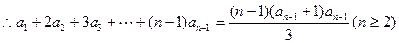
两式相减得:
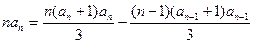
则当
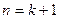 时,
时,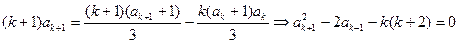
 时,猜想也成立
时,猜想也成立故对一切的
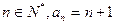 成立
成立(Ⅱ)设
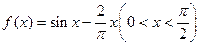
由
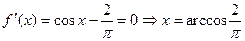
由
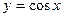 的单调
的单调 性知
性知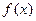 在
在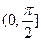 内有且只有一个极大值点,
内有且只有一个极大值点,且
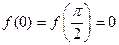
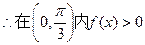
即

令
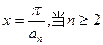 时有
时有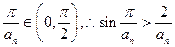
又当
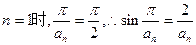
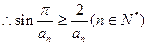
(Ⅲ)
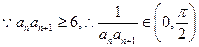
由(Ⅱ)可知
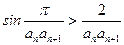
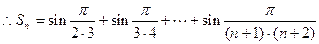
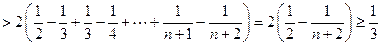
即对一切
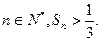
又
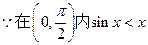
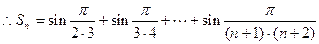
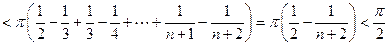
即对一切
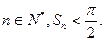
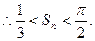

练习册系列答案
相关题目
 ( )
( )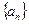 满足,
满足,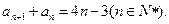
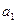 的值;
的值;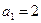 时,求数列
时,求数列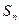 ;
;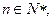 都有
都有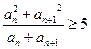 成立,求
成立,求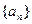 中,
中,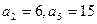 ,若
,若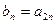 ,则数列
,则数列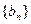 的前5项和等于( )
的前5项和等于( )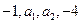 成等差数列,
成等差数列,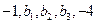 成等比数列,那么
成等比数列,那么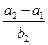 等于( )
等于( )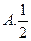
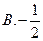
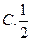 或
或
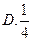
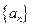 的前n项和为
的前n项和为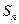 ,若
,若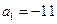 ,
,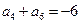 ,则当
,则当 .8 D.9
.8 D.9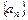 中,
中,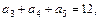 则
则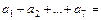 ( )
( ) 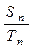 =
=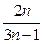 ,则
,则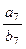 =_______。
=_______。
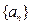 的前5项和
的前5项和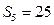 ,且
,且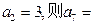 ( )
( )