Question

【题目】如图半圆的直径为4，为直径延长线上一点，且，为半圆周上任一点，以为边作等边（、、按顺时针方向排列）

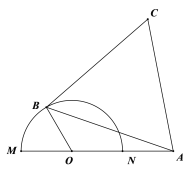
（1）若等边边长为，，试写出关于的函数关系；

（2）问为多少时，四边形的面积最大？这个最大面积为多少？

Answer 1

【答案】（1）；（2）时，四边形OACB的面积最大，其最大面积为．

【解析】

（1）根据余弦定理可求得；

（2）先表示出△ABC的面积及△OAB的面积，进而表示出四边形OACB的面积，并化简函数的解析式为正弦型函数的形式，再结合正弦型函数最值的求法进行求解．

（1）由余弦定理得

则

（2）四边形OACB的面积＝△OAB的面积+△ABC的面积

则△ABC的面积

△OAB的面积

四边形OACB的面积

当，

即时，四边形OACB的面积最大，其最大面积为．