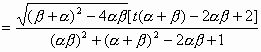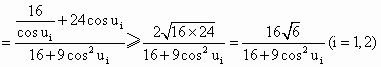题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
解法一:设 所以, 而 因此, 解法二: 由于
所以 故 |
(2) |
因为对任意的 所以 又 所以
由韦达定理知, 于是 |
(3) |
故
显然,上述不等式不能同时取等号, 所以 |

练习册系列答案
相关题目
| |||||||||||